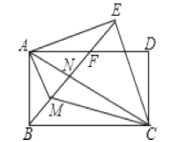
【题目】如图,四边形ABCD为矩形,△ACE为AC为底的等腰直角三角形,连接BE交AD、AC分别于F. N,CM平分∠ACB交BN于M,下列结论:(1)BE⊥ED;(2)AB=AF;(3)EM=EA;(4)AM平分∠BAC,其中正确的结论有( )
A. 1个B. 2个
C. 3个D. 4个
参考答案:
【答案】B
【解析】
连接DE,由∠ABC=∠AEC=∠ADC=90°,根据圆周角定理的推论得到点A、B、C、D、E都在以AC为直径的圆上,再利用矩形的性质可得AE=ME,即①正确;再根据圆周角定理得到∠AEB=∠ACB,∠DAC=∠CED,∠EAD=∠ECD,易证△AEF≌△CED,即可得到AB=AF,即②正确;由②得到∠ABF=∠AFB=45°,求出∠EMC=∠MCB+45°,
而∠ECM=∠NCM+45°,即③正确;根据等腰三角形性质求出∠EAM=∠AME,推出∠EAM=45°+∠MAN,∠AME=45°+∠BAM,即可判断(4).
连接DE.
∵四边形ABCD为矩形,△ACE为AC为底的等腰直角三角形,
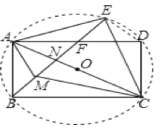
∴∠ABC=∠AEC=∠ADC=90°,AB=CD,AD=BC,
∴点A. B. C. D. E都在以AC为直径的圆上,
∵AB=CD,
∴弧AB=弧CD,
∴∠AEB=∠CED,
∴∠BED=∠BEC+∠CED=∠BEC+∠AEB=90°,
∴BE⊥ED,故(1)正确;
∵点A. B. C. D. E都在以AC为直径的圆上,
∴∠AEF=∠CED,∠EAF=∠ECD,
又∵△ACE为等腰直角三角形,
∴AE=CE,
在△AEF和CED中,
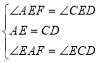 ,
,
∴△AEF≌△CED,
∴AF=CD,
而CD=AB,
∴AB=AF,即(2)正确;
∴∠ABF=∠AFB=45°,
∴∠EMC=∠MCB+45°,
而∠ECM=∠NCM+45°,
∵CM平分∠ACB交BN于M,
∴∠EMC=∠ECM,
∴EC=EM,
∴EM=EA,即(3)正确;
∵AB=AF,∠BAD=90°,EM=EA,
∴∠ABF=∠CBF=45°,∠EAM=∠AME,
∵△AEC是等腰直角三角形,
∴∠EAC=45°,
∴∠EAM=45°+∠MAN,∠AME=∠ABM+∠BAM=45°+∠BAM,
∴∠BAM=∠NAM,∴(4)正确;
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小方家住户型呈长方形,平面图如下(单位:米),现准备铺设地面,三间卧室铺设木地板,其它区城铺设地砖.

(1)求a的值.
(2)铺设地面需要木地板和地砖各多少平方米(用含
 的代数式表示)?
的代数式表示)?(3)按市场价格,木地板单价为300元/平方米,地砖单价为100元/平方米,装修公司有
 两种活动方案,如表:
两种活动方案,如表:活动方案
木地板价格
地砖价格
总安装费
A
8折
8.5折
2000元
B
9折
8.5折
免收
已知卧室2的面积是21平方米,则小方家应选择哪种活动,使铺设地面的总费用(包括材料费及安装费)更低?
-
科目: 来源: 题型:
查看答案和解析>>【题目】宇航员翟志刚在太空进行了19分35秒的舱外活动中,飞行了9 165 000 米,成为中国“飞得最高、走得最快”的人.将9 165 000 米保留两位有效数字用科学记数法记为( )米
A.
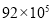 B.
B.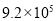 C.
C.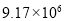 D.
D.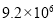
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°③
 (∠α+∠β);④
(∠α+∠β);④ (∠α﹣∠β).正确的有( )
(∠α﹣∠β).正确的有( )A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE.
(1)如图①,当∠BOC=70°时,求∠DOE的度数;
(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠DOE的大小是否发生变化若变化,说明理由;若不变,求∠DOE的度数;
(3)如图③,当射线OC在∠AOB外绕O点旋转时,画出图形,判断∠DOE的大小是否发生变化若变化,说明理由;若不变,求∠DOE的度数.

-
科目: 来源: 题型:
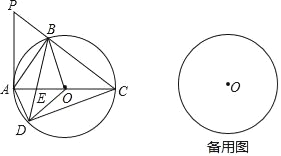
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,⊙O是△ABC外接圆,点D是圆上一点,点D、B分别在AC两侧,且BD=BC,连接AD、BD、OD、CD,延长CB到点P,使∠APB=∠DCB.
(1)求证:AP为⊙O的切线;
(2)若⊙O的半径为1,当△OED是直角三角形时,求△ABC的面积;
(3)若△BOE、△DOE、△AED的面积分别为a、b、c,试探究a、b、c之间的等量关系式,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类。学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图。
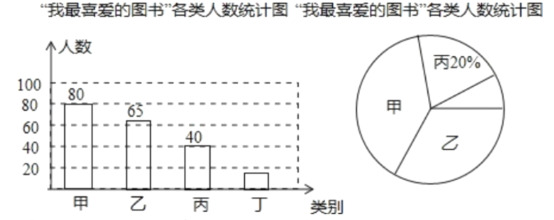
请你结合图中信息,解答下列问题:
(1)本次共调查了___名学生;
(2)被调查的学生中,最喜爱丁类图书的有___人,最喜爱甲类图书的人数占本次被调查人数的___%;
(3)在最喜爱丙类学生的图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生1500人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人。
相关试题

