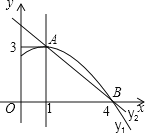
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(-1,0);⑤当1<x<4时,有y2<y1,
其中正确的是( )
A. ①②③ B. ①③④ C. ①③⑤ D. ②④⑤
参考答案:
【答案】C
【解析】试题解析:∵抛物线的顶点坐标A(1,3),
∴抛物线的对称轴为直线x=-![]() =1,
=1,
∴2a+b=0,所以①正确;
∵抛物线开口向下,
∴a<0,
∴b=-2a>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以②错误;
∵抛物线的顶点坐标A(1,3),
∴x=1时,二次函数有最大值,
∴方程ax2+bx+c=3有两个相等的实数根,所以③正确;
∵抛物线与x轴的一个交点为(4,0)
而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点为(-2,0),所以④错误;
∵抛物线y1=ax2+bx+c与直线y2=mx+n(m≠0)交于A(1,3),B点(4,0)
∴当1<x<4时,y2<y1,所以⑤正确.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由边长为1的小正方形组成的格点中,建立如图平面直角坐标系,△ABC的三个顶点坐标分别为A(2,1),B(4,5),C(5,2).
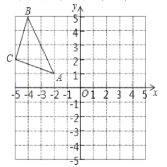
(1)请画出△ABC关于y轴对称的△A
 B
B C
C ;
;(2)画出△ABC关于原点O成中心对称的△A
 B
B C
C ;
;(3)请你判断△AA
 A
A 与△CC
与△CC C
C 的相似比;若不相似,请直接写出△AA
的相似比;若不相似,请直接写出△AA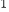 A
A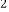 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2
 ,则MN的长为( )
,则MN的长为( )
A.2
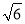 B.4
B.4 C.5 D.6
C.5 D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个长为
 ,宽为
,宽为 的长方形内,该长方形内部未被卡片覆盖的部分用阴影表示.
的长方形内,该长方形内部未被卡片覆盖的部分用阴影表示.
(1)能否用只含
 的式子表示出图②中两块阴影部分的周长和?_____(填“能”或“不能”);(2)若能,请你用只含
的式子表示出图②中两块阴影部分的周长和?_____(填“能”或“不能”);(2)若能,请你用只含 的式子表示出中两块阴影部分的周长和;若不能,请说明理由_____.
的式子表示出中两块阴影部分的周长和;若不能,请说明理由_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明的父亲上星期五买进某公司股票1000股,每股30元,如表为本周内每日该股票的涨跌情况(单位:元)
星期
一
二
三
四
五
每股涨跌
+3
+1.5
-2
-1.5
+1
(1) 星期三收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低每股多少元?
(3)已知小明父亲买进股票时付了1.5‰的手续费,卖出时需付成交额1.5‰的手续费和1‰的交易税,如果他在周五收盘前将全部股票卖出,他的收益情况如何
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b的图象与反比例函数y=
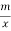 图象相交于点A(﹣1,2)与点B(﹣4,n).
图象相交于点A(﹣1,2)与点B(﹣4,n).(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积.
(3)在第二象限内,求不等式ax+b<
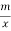 的解集(请直接写出答案).
的解集(请直接写出答案).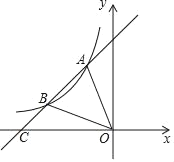
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.

相关试题

