【题目】如图,在平面直角坐标中,点O为坐标原点,直线y=﹣x+4与x轴交于点A,过点A的抛物线y=ax2+bx与直线y=﹣x+4交于另一点B,且点B的横坐标为1.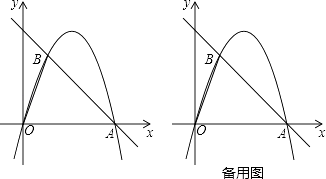
(1)求a,b的值;
(2)点P是线段AB上一动点(点P不与点A、B重合),过点P作PM∥OB交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,过点P作PF⊥MC于点F,设PF的长为t,MN的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,当S△ACN=S△PMN时,连接ON,点Q在线段BP上,过点Q作QR∥MN交ON于点R,连接MQ、BR,当∠MQR﹣∠BRN=45°时,求点R的坐标.
参考答案:
【答案】
(1)解:∵y=﹣x+4与x轴交于点A,
∴A(4,0),
∵点B的横坐标为1,且直线y=﹣x+4经过点B,
∴B(1,3),
∵抛物线y=ax2+bx经过A(4,0),B(1,3),
∴ ![]() ,
,
解得: ![]() ,
,
∴a=﹣1,b=4;
(2)解:方法一:
如图,作BD⊥x轴于点D,延长MP交x轴于点E,
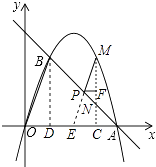
∵B(1,3),A(4,0),
∴OD=1,BD=3,OA=4,
∴AD=3,
∴AD=BD,
∵∠BDA=90°,∠BAD=∠ABD=45°,
∵MC⊥x轴,∴∠ANC=∠BAD=45°,
∴∠PNF=∠ANC=45°,
∵PF⊥MC,
∴∠FPN=∠PNF=45°,
∴NF=PF=t,
∵∠PFM=∠ECM=90°,
∴PF∥EC,
∴∠MPF=∠MEC,
∵ME∥OB,∴∠MEC=∠BOD,
∴∠MPF=∠BOD,
∴tan∠BOD=tan∠MPF,
∴ ![]() =
= ![]() =3,
=3,
∴MF=3PF=3t,
∵MN=MF+FN,
∴d=3t+t=4t;
方法二:
延长MP交x轴于点M′,作M′N′∥MN交AB于N′,
延长FP交M′N′于F′,∵M′N′∥MN,∴△PMN∽△PM′N′,
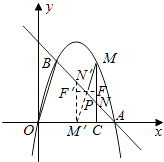
∴ ![]() ,∵O(0,0),B(1,3),
,∵O(0,0),B(1,3),
∴KOB=3,
∵PM∥OB,
∴KPM=KOB=3,则lPM:y=3x+b,设P(p,﹣p+4),则b=4﹣4p,
∴lPM:y=3x+4﹣4P,把y=0代入,∴x= ![]() ,
,
∴M′( ![]() ,0),
,0),
∵N′x=M′x,把x= ![]() 代入y=﹣x+4,
代入y=﹣x+4,
∴y= ![]() ,
,
∴N′( ![]() ,
, ![]() ),∴M′N′=
),∴M′N′= ![]() ,
,
∵PF′⊥M′N′,
∴PF′=p﹣ ![]() =
= ![]() ,
,
∴ ![]() .
.
(3)解:方法一:
如备用图,由(2)知,PF=t,MN=4t,

∴S△PMN= ![]() MN×PF=
MN×PF= ![]() ×4t×t=2t2,
×4t×t=2t2,
∵∠CAN=∠ANC,
∴CN=AC,
∴S△ACN= ![]() AC2,
AC2,
∵S△ACN=S△PMN,
∴ ![]() AC2=2t2,
AC2=2t2,
∴AC=2t,
∴CN=2t,
∴MC=MN+CN=6t,
∴OC=OA﹣AC=4﹣2t,
∴M(4﹣2t,6t),
由(1)知抛物线的解析式为:y=﹣x2+4x,
将M(4﹣2t,6t)代入y=﹣x2+4x得:
﹣(4﹣2t)2+4(4﹣2t)=6t,
解得:t1=0(舍),t2= ![]() ,
,
∴PF=NF= ![]() ,AC=CN=1,OC=3,MF=
,AC=CN=1,OC=3,MF= ![]() ,PN=
,PN= ![]() ,PM=
,PM= ![]() ,AN=
,AN= ![]() ,
,
∵AB=3 ![]() ,
,
∴BN=2 ![]() ,
,
作NH⊥RQ于点H,
∵QR∥MN,
∴∠MNH=∠RHN=90°,∠RQN=∠QNM=45°,
∴∠MNH=∠NCO,
∴NH∥OC,
∴∠HNR=∠NOC,
∴tan∠HNR=tan∠NOC,
∴ ![]() =
= ![]() =
= ![]() ,
,
设RH=n,则HN=3n,
∴RN= ![]() n,QN=3
n,QN=3 ![]() n,
n,
∴PQ=QN﹣PN=3 ![]() n﹣
n﹣ ![]() ,
,
∵ON= ![]() =
= ![]() ,
,
OB= ![]() =
= ![]() ,
,
∴OB=ON,∴∠OBN=∠BNO,
∵PM∥OB,
∴∠OBN=∠MPB,
∴∠MPB=∠BNO,
∵∠MQR﹣∠BRN=45°,∠MQR=∠MQP+∠RQN=∠MQP+45°,
∴∠BRN=∠MQP,
∴△PMQ∽△NBR,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:n= ![]() ,
,
∴R的横坐标为:3﹣ ![]() =
= ![]() ,R的纵坐标为:1﹣
,R的纵坐标为:1﹣ ![]() =
= ![]() ,
,
∴R( ![]() ,
, ![]() ).
).
方法二:
设M(t,﹣t2+4t),N(t,﹣t+4),
∴MN=﹣t2+4t+t﹣4=﹣t2+5t﹣4,
∴PF= ![]() (﹣t2+5t﹣4),
(﹣t2+5t﹣4),
∴S△PMN= ![]() (﹣t2+5t﹣4)2=
(﹣t2+5t﹣4)2= ![]() (t﹣4)2(t﹣1)2,
(t﹣4)2(t﹣1)2,
∵KAB=﹣1,∴∠OAB=45°,
∴CA=CN=4﹣t,
∴S△ACN= ![]() (t﹣4)2,
(t﹣4)2,
∵S△ACN=S△PMN,
∴ ![]() (t﹣4)2(t﹣1)2=
(t﹣4)2(t﹣1)2= ![]() (t﹣4)2,
(t﹣4)2,
∴t1=﹣1,(舍),t2=3,
∴M(3,3),
∵MX=NX=3,
∴N(3,1),
∴ON= ![]() ,
,
∵B(1,3),
∴OB= ![]() ,
,
∴OB=ON,∠OBN=∠ONB,
∵OB∥MP
∴∠OBN=∠QPM,
∴∠ONB=∠QPM,∠RQA=45°,
∵∠MQR﹣∠BRN=45°,
∴∠BRN=∠MQP,
∴△BRN∽△MQP,
∴ ![]() ,
,
∵KPM=3,M(3,3),
∴lPM:y=3x﹣6,
∵lAB:y=﹣x+4,
∴P(2.5,1.5),
设R(3t,t),
∴Q(3t,﹣3t+4),
∴ ![]() ,
,
∴t1= ![]() ,t2=
,t2= ![]() (舍),
(舍),
∴R( ![]() ,
, ![]() ).
).
【解析】先由直线解析式求出A、B坐标,代入抛物线解析式,可求出a、b;(2)利用平行线的性质可推出∠MPF=∠BOD,tan∠BOD=tan∠MPF,用t的代数式表示线段,代入正切定义式中,得出关系式;(3)由已知∠MQR﹣∠BRN=45°,结合平行性质,可得∠BRN=∠MQP,进而证出△BRN∽△MQP,对应边成比例,可列出关于t的方程,求出R坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l:y=
 x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,点B2013的坐标为( )
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,点B2013的坐标为( )
A. (42012×
 ,42012) B. (24026×
,42012) B. (24026×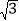 ,24026) C. (24026×
,24026) C. (24026×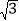 ,24024) D. (44024×
,24024) D. (44024×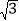 ,44024)
,44024) -
科目: 来源: 题型:
查看答案和解析>>【题目】延庆区由于生态质量良好、自然资源丰富,成为北京的生态涵养区,是其生态屏障和水源保护地.为降低空气污染,919公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年载客量如表:
A型
B型
价格(万元/台)
a
b
年载客量(万人/年)
60
100
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求a,b的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次.请你设计一个方案,使得购车总费用最少. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC(精确到0.1米).
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)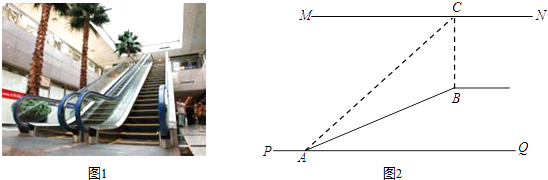
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=30°,BC=2
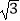 ,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )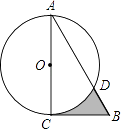
A.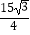 ﹣
﹣ 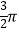
B.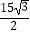 ﹣
﹣ 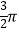
C.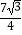 ﹣
﹣ 
D.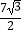 ﹣
﹣ 
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从家骑车上学,先匀速上坡到达
 地后再匀速下坡到达学校,所用的时间与路程如图所示,如果返回时,上、下坡速度仍然保持不变,那么他从学校回到家需要的时间是( )
地后再匀速下坡到达学校,所用的时间与路程如图所示,如果返回时,上、下坡速度仍然保持不变,那么他从学校回到家需要的时间是( )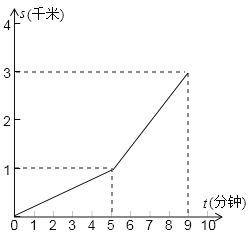
A.9分钟B.12分钟C.8分钟D.10分钟
-
科目: 来源: 题型:
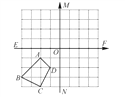
查看答案和解析>>【题目】(齐齐哈尔中考)如图所示,在四边形ABCD中.
(1)画出四边形A1B1C1D1,使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称;
(2)画出四边形A2B2C2D2,使四边形A2B2C2D2与四边形ABCD关于点O中心对称.
(3)四边形A1B1C1D1与四边形A2B2C2D2是否对称,若对称请在图中画出对称轴或对称中心.
相关试题

