【题目】一粒木质中国象棋棋子“車”，它的正面雕刻一个“車”字，它的反面是平的，将棋子从一定高度下抛，落地反弹后可能是“車”字面朝上，也可能是“車”字朝下．由于棋子的两面不均匀，为了估计“車”字朝上的机会，某实验小组做了棋子下抛实验，并把实验数据整理如下：

实验次数

20

40

60

80

100

120

140

160

“車”字朝上的频数

14

18

38

47

52

　

78

88

相应的频率

0.7

0.45

0.63

0.59

0.52

0.55

0.56

　


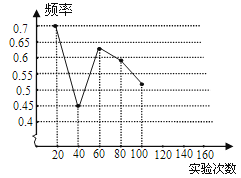
（1）请将表中数据补充完整，并画出折线统计图中剩余部分．
（2）如果实验继续进行下去，根据上表数据，这个实验的频率将接近于该事件发生的机会，请估计这个机会约是多少？
（3）在（2）的基础上，进一步估计：将该“車”字棋子，按照实验要求连续抛2次，则刚好使“車”字一次字面朝上，一次朝下的可能性为多少？

参考答案：

【答案】解：（1）所填数字为：120×0.55=66，88÷160=0.55；
折线图：

（2）如果实验继续进行下去，根据上表数据，这个实验的频率将接近于该事件发生的机会，请估计这个机会约是0.5．
（3）根据（2）的结果估计连续抛2次，则刚好使“車”字一次字面朝上，一次朝下的可能性为0.5．
【解析】（1）根据图中信息，用频数除以实验次数，得到频率，由于试验次数较多，可以用频率估计概率；描点连线，可得折线图 ;
（2）根据表中数据，试验频率为0.7，0.45，0.63，0.59，0.52，0.55，0.56，0.55稳定在0.55左右，即可估计概率的大小;
（3）列举出抛掷两次可能会出现的情况，用概率公式求解即可．

关闭