Question

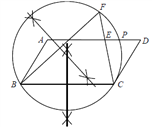
【题目】如图，在平行四边形ABCD中，E是AD上一点，延长CE到点F，使∠FBC=∠DCE ，

(1) 求证∠D=∠F

(2) 用直尺和圆规在AD上作出一点P，使∠BPC=∠D（保留作图痕迹，不写作法）.

Answer 1

【答案】（1）证明见解析；（2）作图见解析.

【解析】试题分析：（1）由AD∥BC得到∠CED＝∠BCF，再由∠DCE＝∠FBC以及三角形内角和定理易用得∠D＝∠F；

（2）作△BCF的外接圆与AD边的交点即为满足条件的点P.

试题解析：（1）∵ 四边形ABCD 是平行四边形，

∴ AD∥BC．

∴ ∠CED＝∠BCF．

∵ ∠CED＋∠DCE＋∠D＝180°，∠BCF＋∠FBC＋∠F＝180°，

∴ ∠D＝180°－∠CED－∠DCE，∠F＝180°－∠BCF－∠FBC．

又∠DCE＝∠FBC，

∴ ∠D＝∠F；

（2）图中P 就是所求作的点．