【题目】如图,Rt△CEF中,∠C=90°,∠CEF, ∠CFE外角平分线交于点A,过点A分别作直线CE、CF的垂线,B、D为垂足.
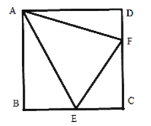
(1)求证:四边形ABCD是正方形,
(2)已知AB的长为6,求(BE+6)(DF+6)的值,
(3)借助于上面问题的解题思路,解决下列问题:若三角形PQR中,∠QPR=45°,一条高是PH,长度为6,QH=2,则HR= .
参考答案:
【答案】(1)见解析;(2)72;(3)3.
【解析】
(1)根据三个角是直角的四边形先证得四边形ABCD是矩形,再过点A作AG⊥EF于点G,根据角平分线的性质得出AB=AG= AD,问题即得解决;
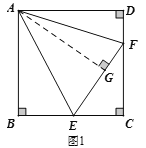
(2)如图1,通过两次运用HL可证得EF=BE+DF,再设BE=x,DF=y,在Rt△CEF中,根据勾股定理得出关于x、y的等式,再整体代入![]() 展开整理后的式子即可得到答案;
展开整理后的式子即可得到答案;
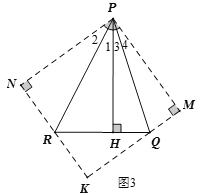
(3)如图3,作△PRH关于PR对称的△PRN,作△PQH关于PQ对称的△PQM,NR和MQ的延长线交于点K,先根据邻边相等的矩形是正方形证明四边形PNKM是正方形,再根据(2)的结论即可求出结果.
解:(1)证明:∵AD⊥CD,AB⊥CB,∠C=90°,
∴四边形ABCD是矩形,
如图1,过点A作AG⊥EF于点G,
∵AF平分∠DFE,AD⊥CD,
∴AG=AD,
同理可得:AG=AB,
∴AB=AD.
∴矩形ABCD是正方形.
(2)在Rt△ADF和Rt△AGF中,
![]()
∴Rt△ADF≌Rt△AGF(HL).
∴DF=GF,
同理可得BE=GE.
∴EF=GE+GF=BE+DF.
设BE=EG=x,DF=FG=y,则CE=6-x,CF=6-y,如图2:

在Rt△CEF中,根据勾股定理得:![]() ,即
,即![]() ,整理得:
,整理得:![]() .
.
∴![]() .
.
(3)如图3,作△PRH关于PR对称的△PRN,作△PQH关于PQ对称的△PQM,NR和MQ的延长线交于点K,则PN=PH=6,PM=PH=6,∠2=∠1,∠4=∠3,∠N=∠PHR=90°,∠M=∠PHQ=90°,MQ=HQ=2,NR=HR,
∴PN=PM=6,
∵∠1+∠3=45°,
∴∠1+∠2+∠3+∠4=90°,即∠NPM=90°,
∴四边形PNKM是正方形.
∵RQ=RH+HQ=NR+QM,
∴由(2)题的结论知:![]() ,
,
即![]() ,解得
,解得![]() ,即HR=3.
,即HR=3.
故答案为3.
-
科目: 来源: 题型:
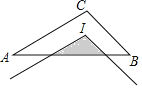
查看答案和解析>>【题目】如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为( )
A. 4.5 B. 4 C. 3 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】春节前小王花1200元从农贸市场购进批发价分别为每箱30元与50元的A,B两种水果进行销售,并分别以每箱35元与60元的价格出售,设购进A水果x箱,B水果y箱.
(1)让小王将水果全部售出共赚了215元,则小王共购进A、B水果各多少箱?
(2)若要求购进A水果的数量不得少于B水果的数量,则应该如何分配购进A, B水果的数量并全部售出才能获得最大利润,此时最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲乙两家商店出售两种同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠,该班现需球拍5副,乒乓球若干盒(不小于5盒).问:
(1)若购买的乒乓球为
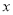 盒,请分别用代数式表示在两家店购买这些乒乓球和乒乓球拍时应该支付的费用;
盒,请分别用代数式表示在两家店购买这些乒乓球和乒乓球拍时应该支付的费用;(2)当购买15盒、30盒乒乓球时,请你去办这件事,你打算去哪家商店购买,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于题目“一段抛物线L:y=﹣x(x﹣3)+c(0≤x≤3)与直线l:y=x+2有唯一公共点,若c为整数,确定所有c的值,”甲的结果是c=1,乙的结果是c=3或4,则( )
A. 甲的结果正确
B. 乙的结果正确
C. 甲、乙的结果合在一起才正确
D. 甲、乙的结果合在一起也不正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一出租车一天下午以鼓楼为出发点在东西方向运营,向东走为正,向西走为负,行车里程(单位:km)依先后次序记录如下:
 .
.(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:5:6,③∠A=90°﹣∠B,④∠A=∠B=
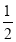 ∠C中,能确定△ABC是直角三角形的条件有( )
∠C中,能确定△ABC是直角三角形的条件有( )A. 1个B. 2个C. 3个D. 4个
相关试题

