【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P与点B、C都不重合),现将△PCD沿直线PD折叠,使点C落到点F处;过点P作∠BPF的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A.
B.
C.
D.
参考答案:
【答案】C
【解析】解:∵∠CPD=∠FPD,∠BPE=∠FPE,
又∵∠CPD+∠FPD+∠BPE+∠FPE=180°,
∴∠CPD+∠BPE=90°,
又∵直角△BPE中,∠BPE+∠BEP=90°,
∴∠BEP=∠CPD,
又∵∠B=∠C,
∴△BPE∽△CDP,
∴ ![]() ,即
,即 ![]() ,则y=﹣
,则y=﹣ ![]() x2+
x2+ ![]() x,y是x的二次函数,且开口向下.
x,y是x的二次函数,且开口向下.
故选:C.
证明△BPE∽△CDP,根据相似三角形的对应边的比相等求得y与x的函数关系式,根据函数的性质即可作出判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升8微克(1000微克=1毫克),接着逐步衰减,10小时时血液中含药量为每毫升4微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示.当成人按规定剂量服药后:
(1)求y与x之间的解析式;
(2)如果每毫升血液中含药量不低于3微克或3微克以上时,在治疗疾病时是有效的,那么这个有效时间是多少小时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
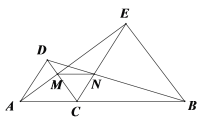
查看答案和解析>>【题目】如图,点C在AB上,△DAC、△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,则下列结论:①AE=DB;②CM=CN;③△CMN为等边三角形;④MN//BC;
正确的有_________(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将油箱注满k升油后,轿车行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系S=
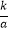 (k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶760千米,当平均耗油量为0.08升/千米时,该轿车可以行驶千米.
(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶760千米,当平均耗油量为0.08升/千米时,该轿车可以行驶千米. -
科目: 来源: 题型:
查看答案和解析>>【题目】太原市公共自行车的建设速度、单日租骑量等四项指标稳居全国首位.公共自行车车桩的截面示意图如图所示,AB⊥AD,AD⊥DC,点B,C在EF上,EF∥HG,EH⊥HG,AB=75cm,AD=24cm,BC=25cm,EH=4cm,则点A到地面的距离是 cm.
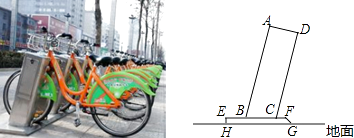
-
科目: 来源: 题型:
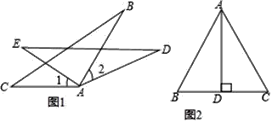
查看答案和解析>>【题目】(1)如图1,AC=AE,∠1=∠2,∠C=∠E.求证:BC=DE.
(2)如图2,在△ABC中,AB=AC,D为BC中点,∠BAD=30°,求∠C的度数.
相关试题

