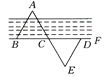
【题目】如图所示,A,B两个建筑物分别位于河的两岸,要测得它们之间的距离,可以从B出发沿河岸画一条射线BF,在BF上截取BC=CD,过D作DE∥AB,使E,C,A在同一条直线卜,则DE的长就等于A,B之间的距离,请你说明道理.
参考答案:
【答案】见解析.
【解析】【试题分析】因为AB∥DE,所以∠A=∠E或∠ABC=∠EDC,因为BC=CD,根据AAS证明ΔABC≌ΔEDC,所以AB=ED.从而得证.
【试题解析】
由题意并结合图形可以知道BC=CD,∠ACB=∠ECD,又AB∥DE,从而∠A=∠E或∠ABC=∠EDC,故在ΔABC与ΔEDC中, 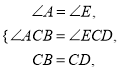 所以ΔABC≌ΔEDC
所以ΔABC≌ΔEDC
(AAS),所以AB=ED,即测出ED的长后即可知道A,B之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:
(1)(
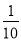 )4×(
)4×(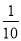 )3×(
)3×(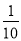 )2;
)2;(2)an-1·an·a;
(3)(-x2)·(x3)·(-x)2;
(4)x2·x5+x·x2·x4;
(5)(x-y)2·(y-x)3+2(x-y)·(x-y)4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
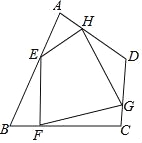
A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形
B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形
C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形
D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣3x+2)(﹣3x﹣2)﹣5x(1﹣x)+(2x+1)(x﹣5)
(2)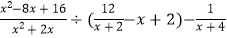 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=(x﹣4)2+2图象的顶点坐标是( )
A.(﹣4,2)B.(4,﹣2)C.(4,2)D.(﹣4,﹣2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,(10分)AB∥DE,试问∠B、∠E、∠BCE有什么关系.

解:∠B+∠E=∠BCE
过点C作CF∥AB,
则
 ____( )
____( )又∵AB∥DE,AB∥CF,
∴____________( )
∴∠E=∠____( )
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(0,4),B(7,0),C(7,4),连接AC,BC得到矩形AOBC,点D的边AC上,将边OA沿OD折叠,点A的对应边为A'.若点A'到矩形较长两对边的距离之比为1:3,则点A'的坐标为 .
相关试题

