【题目】数学活动课上,励志学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
在证明这道题时,励志学习小组成员小颖同学进行如下书写,请你将此证明过程补充完整
证明:设DH=x,由由题意,CD=2x,CH=![]() x,
x,
∴AD=2AB=4x,
∴AH=AD﹣DH=3x,
∵CH⊥AD,
∴AC=![]() =2
=2![]() x,
x,
(3)深入探究
在(2)的条件下,励志学习小组成员小漫同学探究发现![]() ,试判断小漫同学的结论是否正确,并说明理由
,试判断小漫同学的结论是否正确,并说明理由

参考答案:
【答案】(1)①见解析,②见解析;(2)见解析;(3)正确
【解析】(1)先证△ABC,△ACD都是等边三角形,再证△BCE和△ACF全等即可;
(2)先证△ACE∽△HCF,再利用相似三角形的性质即可得出答案;
(3)利用(2)中证得的结论利用等量代换即可得出答案.
解:(1)①∵四边形ABCD是平行四边形,∠BAD=120°,
∴∠D=∠B=60°,
∵AD=AB,
∴△ABC,△ACD都是等边三角形,
∴∠B=∠CAD=60°,∠ACB=60°,BC=AC,
∵∠ECF=60°,
∴∠BCE+∠ACE=∠ACF+∠ACE=60°,
∴∠BCE=∠ACF,
在△BCE和△ACF中,
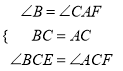 ,
,
∴△BCE≌△ACF.
②∵△BCE≌△ACF,
∴BE=AF,
∴AE+AF=AE+BE=AB=AC.
(2)∴AC2+CD2=AD2,
∴∠ACD=90°,
∴∠BAC=∠ACD=90°,
∴∠CAD=30°,
∴∠ACH=60°,
∵∠ECF=60°,
∴∠HCF=∠ACE,
∴△ACE∽△HCF,
∴![]() =2,
=2,
∴AE=2FH.
(3)结论正确
如图2中,由(2)可知,设![]() ,则
,则![]() ,设
,设![]() ,则
,则![]() ,易知
,易知![]() ,∴
,∴![]() ,∴
,∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将A,B,C,D四人随机分成甲、乙两组参加羽毛球比赛,每组两人。
(1)A在甲组的概率是多少?
(2)A,B都在甲组的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线
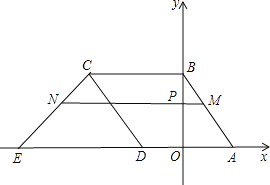
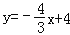 与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.
与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.①请直接写出点C、点D的坐标,并求出m的值;
②点P(0,t)是线段OB上的一个动点(点P不与O、B重合),经过点P且平行于x轴的直线交AB于M、交CE于N.设线段MN的长度为d,求d与t之间的函数关系式(不要求写自变量的取值范围);
③点P(0,t)是y轴正半轴上的一个动点,为何值时点P、C、D恰好能组成一个等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中AB=15,AC=13,高AD=12,则△ABC的周长为( )
A. 42B. 32C. 42或32D. 38或32
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017贵州省遵义市)如图,抛物线
 (a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为
(a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为 .
.(1)求该抛物线的函数关系式与C点坐标;
(2)已知点M(m,0)是线段OA上的一个动点,过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,当m为何值时,△BDE恰好是以DE为底边的等腰三角形?
(3)在(2)问条件下,当△BDE恰好是以DE为底边的等腰三角形时,动点M相应位置记为点M′,将OM′绕原点O顺时针旋转得到ON(旋转角在0°到90°之间);
①探究:线段OB上是否存在定点P(P不与O、B重合),无论ON如何旋转,
 始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;
始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;②试求出此旋转过程中,(NA+
 NB)的最小值.
NB)的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的2016年6月份的日历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )

A. 27 B. 51 C. 69 D. 72
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从A、B两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为2:3,甲、乙两车离AB中点C路程y(千米)与甲车出发时间t(小时)的关系图象如图所示,则下列说法:①A、B两地之间的距离为180千米;②乙车的速度为36千米/小时;③a=3.75;④当乙车到达终点时,甲车距离终点还有30千米.其中正确的结论有( )
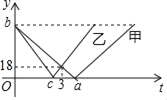
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

