【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做等邻边四边形.
(1)如图1,四边形ABCD中,AC平分∠BAD,∠B=∠D.求证:四边形ABCD为等邻边四边形.
(2)如图2,Rt△ABC中,∠ABC=90°,AB=2,BC=1,将△ABC沿∠ABC的平分线BB′的方向平移,得到△A′B′C′,连接AA′、BC′,若平移后的四边形ABC′A′是等邻边四边形,且满足BC′=AB,求平移的距离.
(3)如图3,在等邻边四边形ABCD中,AB=AD,∠BAD+∠BCD=90°,AC和BD为四边形对角线,△BCD为等边三角形,试探究AC和AB的数量关系.

参考答案:
【答案】(1)证明见解析;(2)平移的距离是![]() ;(3)AC=
;(3)AC=![]() AB,理由见解析.
AB,理由见解析.
【解析】(1)∵∠BAC=∠DAC ,∠B=∠D,AC=AC
∴△ABC≌△ADC
∴AB=AD
∴四边形ABCD是等邻边四边形.---------------------3’
(2)如图,延长C’B’交AB于点D ,
∵△A’B’C’由△ABC平移得到
∴A’B’∥AB,∠ A’B’C’=∠ABC=90°,C’B’=CB=1
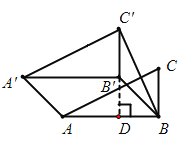
∴B’D⊥AB
∵BB’平分∠ABC,
∴∠B’BD=45°,即B’D=BD。
设B’D=BD=![]() ,∴C’D=1+
,∴C’D=1+![]() ,
,
∵BC’=AB=2,
∴Rt△BDC’中,![]() ,
,
解得![]() =
=![]() ,
,![]() (不合题意,舍去)
(不合题意,舍去)
∴等腰Rt △BB’D中,BB’=![]() =
=![]()
(3)AC=![]() AB。
AB。
理由:如图,过A作AE⊥AB,且AE=AB,连接ED,EB
∵AE⊥AB
∴∠EAD+∠BAD=90°
又∵∠BAD+∠BCD=90°,△BCD为等边三角形
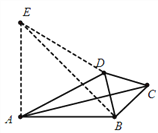
∴∠EAD=∠DCB=60°,
∵AE=AB,AB=AD ∴AE=AD
∴△AED为等边三角形,
∴AD=ED,∠EDA=∠BDC=60°
∴∠BDE=∠CDA,∵ED=AD,BD=CD
∴△BDE≌△CDA
∴AC=BE
∵AE=BE,∠BAE=90°, ∴BE=![]() AB,
AB,
∴AC=![]() AB
AB
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=
 (x>0)的图象上,点D的坐标为(4,3).
(x>0)的图象上,点D的坐标为(4,3).(1)求k的值;
(2)将这个菱形沿x轴正方向平移,当顶点D落在反比例函数图象上时,求菱形平移的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:3x﹣6(x﹣1)=3﹣2(x+3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年4月21日在深圳体育馆召开的第八届中国(深圳)国际茶业文化博览会上某茶商将甲、乙两种茶叶卖出,甲种茶叶卖出1200元,盈利20%,乙种茶叶卖出1200元,亏损20%,则此人在这次交易中是( )
A.盈利50元
B.盈利100元
C.亏损150元
D.亏损100元 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各对量中,不具有相反意义的是( )
A.胜3局与负3局
B.收入3000元与增加3000元
C.气温升高4℃与气温降低10℃
D.转盘逆时针转3圈与顺时针转5圈 -
科目: 来源: 题型:
查看答案和解析>>【题目】中学生上学带手机的现象越来越受到社会的关注,为此媒体记者随机调查了某校若干名学生上学带手机的目的,分为四种类型:A接听电话;B收发短信;C查阅资料;D游戏聊天.并将调查结果绘制成图1和图2的统计图(不完整),请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图1、图2补充完整;
(3)现有4名学生,其中A类两名,B类两名,从中任选2名学生,求这两名学生为同一类型的概率(用列表法或树状图法).

-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P在X轴的上方,Y轴的左侧,且到X轴的距离为3,到Y轴的距离为4,则点P的坐标是___.
相关试题

