【题目】【阅读理解】对于任意正实数a、b,∵(![]() -
-![]() )2≥0,∴a+b-2
)2≥0,∴a+b-2![]() ≥0,
≥0,
∴a+b≥2![]() ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
【数学认识】在a+b≥2![]() (a、b均为正实数)中,若ab为定值k,则a+b≥2
(a、b均为正实数)中,若ab为定值k,则a+b≥2![]() ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2![]()
【解决问题】
(1)若x>0时,x+![]() 有最小值为 ,此时x= ;
有最小值为 ,此时x= ;
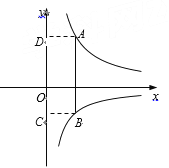
(2)如上图,已知点A在反比例函数y![]() (x>0)的图像上,点B在反比例函数y
(x>0)的图像上,点B在反比例函数y![]() (x>0)的图像上,AB∥y轴,过点A作AD⊥y轴于点 D,过点B作BC⊥y轴于点C.求四边形ABCD周长的最小值
(x>0)的图像上,AB∥y轴,过点A作AD⊥y轴于点 D,过点B作BC⊥y轴于点C.求四边形ABCD周长的最小值
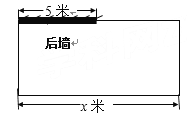
(3)学校准备在图书馆后面的场地上建一个面积为100平方米的长方形自行车棚.图书馆的后墙只有5米长可以利用,其余部分由铁围栏建成,如下图是小尧同学设计的图纸,设所需铁围栏L米,自行车棚长为x米.L是否存在最小值,如果存在,那么当x为何值时,L最小,最小为多少米?如果不存在,请说明理由.
参考答案:
【答案】(1)2,1.(2)12(3)当x为10时,L最小,最小为35米.
【解析】试题分析:(1)根据题意,利用完全平方式即可求解;
(2)根据反比例函数的解析式,设出A和B的坐标,然后表示出周长,再根据上面的知识求解即可;
(3)根据题意列出L的解析式,然后根据阅读理解的内容求解即可.
试题解析:(1)2,1.
(2)解:设A(a,![]() ),则B(a,-
),则B(a,-![]() ),
),
∴四边形ABCD周长=2(a+![]() )
)
≥2×2![]() =4×3=12
=4×3=12
(3)∵L=2x-5+![]() ≥2
≥2![]() -5=35
-5=35
当2x=![]() ,即x=10时,L最小.
,即x=10时,L最小.
答:当x为10时,L最小,最小为35米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中, △ABC三个顶点的位置如图(每个小正方形的边长均为1).
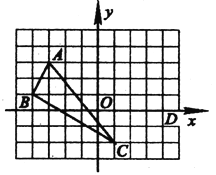
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′、B′、C′三点的坐标:
A′(___________); B′(___________);C′(___________)。
(3)求△ABC的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一个底角是30°,则它的顶角是( )
A.30°
B.40°
C.75°
D.120° -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式不正确的是( )
A. |﹣2|=2 B. ﹣2=﹣|﹣2| C. ﹣(﹣2)=|﹣2| D. ﹣|2|=|﹣2|
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(4,-3)到x轴的距离为( )
A.4B.3C.5D.-3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司要把3000吨货物从M市运到W市.(每日的运输量为固定值)
(1)从运输开始,每天运输的货物吨数y(单位:吨)与运输时间x(单位:天)之间有怎样的函数关系式?
(2)因受到沿线道路改扩建工程影响,实际每天的运输量比原计划少20%,以致推迟1天完成运输任务,求原计划完成运输任务的天数.
-
科目: 来源: 题型:
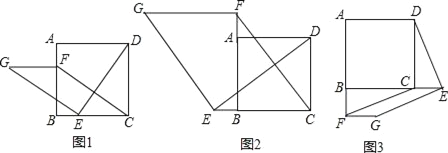
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的数量关系和位置关系;(不要求证明)
(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请给出判断并予以证明;
(3)如图3,若点E、F分别是BC、AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
相关试题

