【题目】如图,正方形ABCD的边长为13,以CD为斜边向外作Rt△CDE.若点A到CE的距离为17,则CE= . 
参考答案:
【答案】12或5
【解析】解:作AF⊥CE于F,DM⊥AF于M,如图所示:
则四边形DEFM是矩形,AF=17,∠AMD=90°,
∴∠EDM=90°,
∵四边形ABCD是正方形,
∴AD=CD=13,∠ADC=∠EDM=90°,
∴∠ADM=∠CDE,
在△ADM和△CDE中, 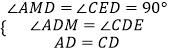 ,
,
∴△ADM≌△CDE(AAS),
∴DM=DE,AM=CE,
∴四边形DEFM是正方形,
∴DM=FM,
设AM=CE=x,则DM=FM=17﹣x,
在Rt△ADM中,由勾股定理得:x2+(17﹣x)2=132,
解得:x=12或x=5,
∴CE=12,或CE=5;
故答案为:12或5.
作AF⊥CE于F,DM⊥AF于M,由AAS证明△ADM≌△CDE,得出DM=DE,AM=CE,证出四边形DEFM是正方形,得出DM=FM,设AM=CE=x,则DM=FM=17﹣x,在Rt△ADM中,由勾股定理得出方程,解方程即可.
-
科目: 来源: 题型:
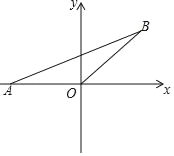
查看答案和解析>>【题目】如图,等腰△AOB中,AO=BO=2,点A在x轴上,OB与x轴的夹角为45°;
(1)求直线AB、OB的解析式;
(2)若将△AOB沿着x轴翻折再向右平移两个单位求直线AB的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字,现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y).
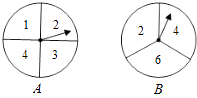
(1)请用列表或画树状图的方法写出所有可能得到的点P的坐标;
(2)李刚为甲、乙两人设计了一个游戏:记s=x+y.当s<6时,甲获胜,否则乙获胜.你认为这个游戏公平吗?对谁有利?
(3)请你利用两个转盘,设计一个公平的游戏规则. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )

A.乙到达B地时甲距A地120km
B.乙出发1.8小时被甲追上
C.甲,乙相距20km时,t为2.4h
D.甲的速度是乙的速度的 倍
倍 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )

A. 24° B. 30° C. 32° D. 36°
-
科目: 来源: 题型:
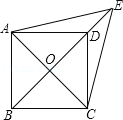
查看答案和解析>>【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时
 张用A方法,其余用B方法。
张用A方法,其余用B方法。(1)用
 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
相关试题

