【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对
他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:s2=![]() [
[![]() ])
])
参考答案:
【答案】解:(1)9;9.
(2)s2甲=![]() ;
;
s2乙=![]() .
.
(3)推荐甲参加比赛更合适.
【解析】
解:(1)9;9.
(2)s2甲=![]()
=![]() =
=![]() ;
;
s2乙=![]()
=![]() =
=![]() .
.
(3)推荐甲参加全国比赛更合适,理由如下:两人的平均成绩相等,说明实力相当;但甲的六次测试成绩的方差比乙小,说明甲发挥较为稳定,故推荐甲参加比赛更合适.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学用两个完全相同的直角三角形纸片重叠在一起(如图1)固定△ABC不动,将△DEF沿线段AB向右平移.
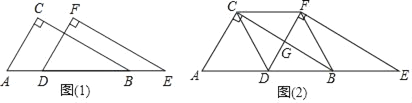
(1)若∠A=60°,斜边AB=4,设AD=x(0≤x≤4),两个直角三角形纸片重叠部分的面积为y,试求出y与x的函数关系式;
(2)在运动过程中,四边形CDBF能否为正方形,若能,请指出此时点D的位置,并说明理由;若不能,请你添加一个条件,并说明四边形CDBF为正方形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】求证:角平分线上的点到这个角的两边的距离相等.
要求:(1)尺规作图:作∠AOB的角平分线,并在该角平分线上取点P,作PM⊥OA于点M,PN⊥OB于点N(不写作法,保留作图痕迹);
(2)以下是结合要证的命题和图形写出的已知,求证,请你完成证明过程.
已知:如图,OP平分∠AOB,PM⊥OA于点M,PN⊥OB于点N.
求证:PM=PN
证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了更好保障居民饮用水安全,环保局决定购10台污水处理设备,现有A、B两种型号的设备,价格与每台日处理污水的能力见下表.

(1)若县环保局购买污水处理设备的资金不超过105万元,你认为有哪几种方案.
(2)在(1)的条件下,每日要求处理污水量不低于2040吨,为了节约资金,请设计“一个最省钱”的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验室里,水平圆桌面上有甲乙丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两根相同的管子在容器的5cm高度处连接(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位高度为
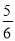 cm,则开始注入________分钟的水量后,甲与乙的水位高度之差是
cm,则开始注入________分钟的水量后,甲与乙的水位高度之差是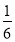 cm.
cm.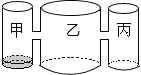
-
科目: 来源: 题型:
查看答案和解析>>【题目】若三个互不相等的有理数既可表示为1,a+b,a的形式,又可表示为0,
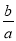 ,b的形式,则12a2﹣5ab=_____.
,b的形式,则12a2﹣5ab=_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

相关试题

