【题目】数轴上有![]() 、
、![]() 、
、![]() 三点,分别表示有理数
三点,分别表示有理数![]() 、
、![]() 、
、![]() ,动点
,动点![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 个单位的速度向右移动,当
个单位的速度向右移动,当![]() 点运动到
点运动到![]() 点时运动停止,设点
点时运动停止,设点![]() 移动时间为
移动时间为![]() 秒.
秒.

(1)用含![]() 的代数式表示
的代数式表示![]() 点对应的数:_________;
点对应的数:_________;
(2)当![]() 点运动到
点运动到![]() 点时,点
点时,点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位的速度向
个单位的速度向![]() 点运动,
点运动, ![]() 点到达
点到达![]() 点后,再立即以同样的速度返回
点后,再立即以同样的速度返回![]() 点.
点.
①用含![]() 的代数式表示
的代数式表示![]() 点在由
点在由![]() 到
到![]() 过程中对应的数:_________;
过程中对应的数:_________;
②当![]() ______时,动点
______时,动点![]() 、
、![]() 到达同一位置(即相遇);
到达同一位置(即相遇);
③当![]() 时,求
时,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() (2)①
(2)①![]()
②当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ③
③![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
【解析】试题分析:(1)根据两点间的距离,可得P到点A和点C的距离;
(2)①根据两点运动的速度和距离之间的关系,可以求出PQ两点间的距离;
②分为返回前相遇和返回后相遇两种情况:返回前相遇,P的路程等于Q的路程等于Q的路程减去16;而返回后相遇,则是二者走的总路程是Q到C的路程的2倍,分别列式子求解.
试题解析:(1)![]() 点所对应的数为:
点所对应的数为: ![]()
(2)①![]()
②![]() 点从
点从![]() 运动到
运动到![]() 点所花的时间为
点所花的时间为![]() 秒,
秒, ![]() 点从
点从![]() 运动到
运动到![]() 点所花的时间为
点所花的时间为![]() 秒
秒
当![]() 时,
时, ![]() :
: ![]() ,
, ![]() :
: ![]()
![]() ,解之得
,解之得![]()
当![]() 时,
时, ![]() :
: ![]() ,
, ![]() :
: ![]()
![]() ,解之得
,解之得![]()
③![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.
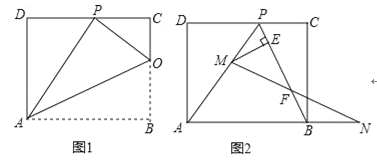
(1)如图1,已知折痕与边BC交于点O,连接AP、OP、OA.
①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长.
(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;
(3)如图2,在(1)的条件下,擦去折痕AO,线段OP,连结BP,动点M在线段AP⊥(点M与点F、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;说明理由;若不变,求出线段EF的长度.
-
科目: 来源: 题型:
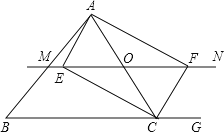
查看答案和解析>>【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由;
(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AECF是正方形.直接写出答案,不需说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需________根火柴( )

A. 156 B. 157 C. 158 D. 159
-
科目: 来源: 题型:
查看答案和解析>>【题目】由a+3=b变为2(a+3)-5=2b-5,其过程中所用等式的性质及顺序是( )
A. 先用等式的性质1,再用等式的性质2
B. 先用等式的性质2,再用等式的性质1
C. 仅用了等式的性质1
D. 仅用了等式的性质2
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简a4b3÷(ab)3的结果是=
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x(x+3)=x+3的根为( )
A. x=﹣3 B. x=1 C. x1=1,x2=3 D. x1=1,x2=﹣3
相关试题

