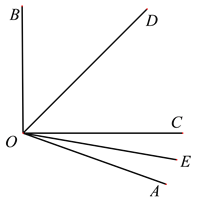
【题目】如图,∠AOB=110°,OD平分∠BOC,OE平分∠AOC。
(1)求∠EOD的度数。
(2)若∠BOC=90°,求∠AOE的度数。
参考答案:
【答案】(1)55゜, (2)10゜
【解析】试题分析:(1)根据OD平分∠BOC,OE平分∠AOC可知∠DOE=∠DOC+∠EOC=
![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB,由此即可得出结论;
∠AOB,由此即可得出结论;
(2)先根据∠BOC=90°求出∠AOC的度数,再根据角平分线的定义即可得出结论.
试题解析:(1)∵∠AOB=110°,OD平分∠BOC,OE平分∠AOC,
∴∠EOD=∠DOC+∠EOC=![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB=
∠AOB=![]() ×110°=55°;
×110°=55°;
(2)∵∠AOB=110°,∠BOC=90°,
∴∠AOC=110°-90°=20°,
∵OE平分∠AOC,
∴∠AOE=![]() ∠AOC=
∠AOC=![]() ×1=20°=10°.
×1=20°=10°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的一边等于3,一边等于7,那么它的周长等于( )
A. 13 B. 13或17 C. 17 D. 14或17
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,点O为原点,A、B为数轴上两点,AB=15,且OA:OB=2.
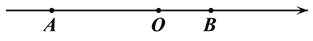
(1)A、B对应的数分别为 、 ;
(2)点A、B分别以4个单位/秒和3个单位/秒的速度相向而行,则几秒后A、B相距1个单位长度?
(3)点A、B以(2)中的速度同时向右运动,点P从原点O以7个单位/秒的速度向右运动,是否存在常数m,使得
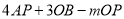 为定值,若存在请求出m值以及这个定值;若不存在,请说明理由.
为定值,若存在请求出m值以及这个定值;若不存在,请说明理由. -
科目: 来源: 题型:
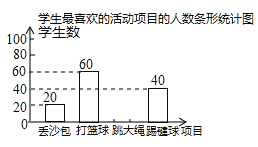
查看答案和解析>>【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表
项目
学生数(名)
百分比
丢沙包
20
10%
打篮球
60
p%
跳大绳
n
40%
踢毽球
40
20%
根据图表中提供的信息,解答下列问题:
(1)m= ,n= ,p= ;
(2)请根据以上信息直接补全条形统计图;
(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程-3x+5=2x-1,移项正确的是( )
A. 3x-2x=-1+5 B. -3x-2x=5-1
C. 3x-2x=-1-5 D. -3x-2x=-1-5
-
科目: 来源: 题型:
查看答案和解析>>【题目】1张新版百元的人民币厚约为0.00009米,数据“0.00009米”用科学记数法可表示为( )
A. 9×10-5米
B.9×10-4米
C.0.9×10-6米
D.90×10-3米 -
科目: 来源: 题型:
查看答案和解析>>【题目】有一人患了某种流感,在每轮传染中平均一个人传染x个人,在进入第二轮传染之前有两人被及时隔离治疗并治愈,若两轮传染后还有24人患流感,则x=______.
相关试题

