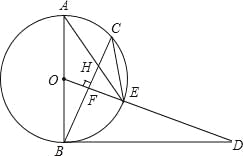
【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的直径为5,sinA=![]() ,求BH的长.
,求BH的长.
参考答案:
【答案】(1)证明见试题解析;(2)证明见试题解析;(3)![]() .
.
【解析】试题分析:(1)由圆周角定理和已知条件证出∠ODB=∠ABC,再证出∠ABC+∠DBF=90°,即∠OBD=90°,即可得出BD是⊙O的切线;
(2)连接AC,由垂径定理得出![]() ,得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例
,得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例![]() ,即可得出结论;
,即可得出结论;
(3)连接BE,由圆周角定理得出∠AEB=90°,由三角函数求出BE,再根据勾股定理求出EA,得出BE=CE=6,由(2)的结论求出EH,然后根据勾股定理求出BH即可.
试题解析:(1)∵∠ODB=∠AEC,∠AEC=∠ABC,∴∠ODB=∠ABC,
∵OF⊥BC,∴∠BFD=90°,∴∠ODB+∠DBF=90°,∴∠ABC+∠DBF=90°,
即∠OBD=90°,∴BD⊥OB,∴BD是⊙O的切线;
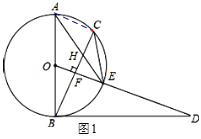
(2)连接AC,如图1所示:
∵OF⊥BC,∴![]() , ∴∠CAE=∠ECB,
, ∴∠CAE=∠ECB,
∵∠CEA=∠HEC,∴△CEH∽△AEC,∴![]() ,∴CE2=EHEA;
,∴CE2=EHEA;
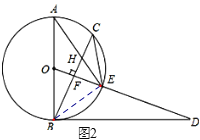
(3)连接BE,如图2所示:
∵AB是⊙O的直径,∴∠AEB=90°,
∵⊙O的半径为![]() ,sin∠BAE=
,sin∠BAE=![]() ,∴AB=5,BE=ABsin∠BAE=5×
,∴AB=5,BE=ABsin∠BAE=5×![]() =3,∴EA=
=3,∴EA=![]() =4,
=4,
∵![]() ,∴BE=CE=3,∵CE2=EHEA,∴EH=
,∴BE=CE=3,∵CE2=EHEA,∴EH=![]()
∴在Rt△ BEH中,BH=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】唐山质量监督局从某食品厂生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,把超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值(单位:克)
﹣6
﹣2
0
1
3
4
袋数
1
4
3
4
5
3
(1)若每袋食品的标准质量为450克,则抽样检测的20袋食品的总质量是多少克?
(2)若该种食品的合格标准为450±5克,求该种食品抽样检测的合格率?
-
科目: 来源: 题型:
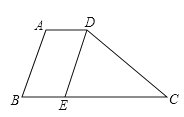
查看答案和解析>>【题目】如图,在梯形ABCD中,AD//BC, ∠B=70°∠C=40°,DE//AB交BC于点E.若AD=3,BC=10,则CD的长是( )
A.7
B.10
C.13
D.14 -
科目: 来源: 题型:
查看答案和解析>>【题目】能判定四边形是平行四边形的条件是( )
A.一组对边平行,另一组对边相等
B.一组对边相等,一组邻角相等
C.一组对边平行,一组邻角相等
D.一组对边平行,一组对角相等 -
科目: 来源: 题型:
查看答案和解析>>【题目】用三个正多边形镶嵌成一个平面时,若前两种是正方形和正六边形,则第三种是( )
A. 正十二边形 B. 正十边形 C. 正八边形 D. 正三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市计划经销一些特产,经销前,围绕“A:王高虎头鸡,B:羊口咸蟹子,C:桂河芹菜,D:巨淀湖咸鸭蛋”四种特产,在全市范围内随机抽取了部分市民进行问卷调查:“我最喜欢的特产是什么?”(必选且只选一种).现将调查结果整理后,绘制成如图所示的不完整的扇形统计图和条形统计图.

(1)请补全扇形统计图和条形统计图;
(2)若全市有110万市民,估计全市最喜欢“羊口咸蟹子”的市民约有多少万人?
(3)在一个不透明的口袋中有四个分别写上四种特产标记A、B、C、D的小球(除标记外完全相同),随机摸出一个小球然后放回,混合摇匀后,再随机摸出一个小球,则两次都摸到A的概率是多少?写出分析计算过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是本地区一种产品30天的销售图象,产品日销售量y(单位:件)与时间t(单位:天)的大致函数关系如图①,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )
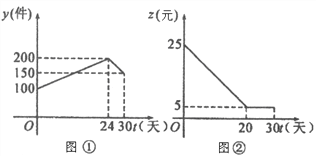
A. 日销售量为150件的是第12天与第30天
B. 第10天销售一件产品的利润是15元
C. 从第1天到第20天这段时间内日销售利润将先增加再减少
D. 第18天的日销售利润是1225元
相关试题

