【题目】如图,∠AOB=90°,∠AOC为∠AOB外的一个锐角,且∠AOC=30°,射线OM平分∠BOC,ON平分∠AOC.
(1)求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠AOC=β(β为锐角),其他条件不变,求∠MON的度数.

参考答案:
【答案】(1)45°(2)![]() α(3)45°
α(3)45°
【解析】
(1)要求∠MON,即求∠COM-∠CON,再根据角平分线的概念分别进行计算即可求得;
(2)和(3)均根据(1)的计算方法进行推导即可.
解:(1)∵∠AOB=90°,∠AOC=30°,
∴∠BOC=120°.
∵OM平分∠BOC,ON平分∠AOC,
∴∠COM=60°,∠CON=15°,
∴∠MON=∠COM-∠CON=45°;
(2)∵∠AOB=α,∠AOC=30°,
∴∠BOC=α+30°.
∵OM平分∠BOC,ON平分∠AOC,
∴∠COM=![]() α+15°,∠CON=15°,
α+15°,∠CON=15°,
∴∠MON=∠COM-∠CON=![]() α;
α;
(3)∵∠AOB=90°,∠AOC=β,
∴∠BOC=90°+β.
∵OM平分∠BOC,ON平分∠AOC,
∴∠COM=45°+![]() β,∠CON=
β,∠CON=![]() β,
β,
∴∠MON=∠COM-∠CON=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间有60个工人,生产甲、乙两种零件,每人每天平均能生产甲种零件24个或乙种零件12个.已知每2个甲种零件和3个乙种零件配成一套,问应分配多少人生产甲种零件,多少人生产乙种零件,才能使每天生产的这两种零件刚好配套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=BC,△ABC≌△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点,观察并猜想线段EA1与FC有怎样的数量关系?并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,转盘A、B中各个扇形的面积相等,且分别标有数字.小明和小丽玩转转盘游戏,规则如下:分别转动转盘A、B,当转盘停止转动时,将两个指针所指扇形内的数字相乘(若指针停在等分线上,那么重转一次).

(1)用列表法(或树状图)分别求出数字之积为3的倍数及数字之积为5的倍数的概率;
(2)小亮和小丽想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小亮得3分;数字之积为5的倍数时,小丽得4分,这个游戏对双方公平吗?请说明理由;认为不公平的,请你修改得分规定,使游戏双方公平. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:已知Q、K、R为数轴上三点,若点K到点Q的距离是点K到点R的距离的2倍,我们就称点K是有序点对
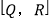 的好点.
的好点.根据下列题意解答问题:
(1)如图1,数轴上点Q表示的数为1,点P表示的数为0,点K表示的数为1,点R表示的数为2.因为点K到点Q的距离是2,点K到点R的距离是1,所以点K是有序点对
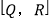 的好点,但点K不是有序点对
的好点,但点K不是有序点对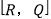 的好点.同理可以判断:点P是不是有序点对
的好点.同理可以判断:点P是不是有序点对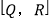 的好点;
的好点; (2)如图2,数轴上点M表示的数为-1,点N表示的数为5,点H表示的数为x,若点H是有序点对
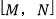 的好点,求x的值;
的好点,求x的值;(3)如图3,数轴上点A表示的数为20,点B表示的数为10.现有一只电子蚂蚁C从点B出发,以每秒3个单位的速度向左运动t秒(t>0).当点A、B、C中恰有一个点为其余两有序点对的好点,直接写出t的所有可能的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,已知点C在线段AB上,线段AC=6,BC=4,点M、N分别是AC、BC的中点,求MN的长度;
(2)根据(1)的计算过程与结果,设AC+BC=a,其它条件不变,请猜想出MN的长度吗?并说明理由;
(3)对于(1)题,如果将“点C在线段AB上”改为“点C在射线AB上”,其它条件不变,求MN的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂生产一种西装和领带,西装每套定价1000元,领带每条定价200元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一套西装送一条领带;②西装和领带都按定价的90%付款.现某客户要到该服装厂购买西装20套,领带x条(x>20).
(1)若该客户按方案①购买,需付款多少元;(用含x的代数式表示)若该客户按方案②购买,需付款多少元.(用含x的代数式表示)
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当x=30,你能给出一种更为省钱的购买方案吗?若有,请写出你的购买方案和总费用;若无,请说明理由.
相关试题

