【题目】如图,转盘A、B中各个扇形的面积相等,且分别标有数字.小明和小丽玩转转盘游戏,规则如下:分别转动转盘A、B,当转盘停止转动时,将两个指针所指扇形内的数字相乘(若指针停在等分线上,那么重转一次). 
(1)用列表法(或树状图)分别求出数字之积为3的倍数及数字之积为5的倍数的概率;
(2)小亮和小丽想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小亮得3分;数字之积为5的倍数时,小丽得4分,这个游戏对双方公平吗?请说明理由;认为不公平的,请你修改得分规定,使游戏双方公平.
参考答案:
【答案】
(1)解:每次游戏可能出现的所有结果列表如下:
4 | 5 | 6 | |
1 | (1,4) | (1,5) | (1,6) |
2 | (2,4) | (2,5) | (2,6) |
3 | (3,4) | (3,5) | (3,6) |
可得表格中共有9种等可能的结果,
则数字之积为3的倍数的有五种,其概率为 ![]() ;数字之积为5的倍数的有三种,其概率为
;数字之积为5的倍数的有三种,其概率为 ![]() =
= ![]()
(2)解:这个游戏对双方不公平,
∵小亮平均每次得分为 ![]() ×3=
×3= ![]() ,小丽平均每次得分为
,小丽平均每次得分为 ![]() ×4=
×4= ![]() ,
,
∵ ![]() ≠
≠ ![]() ,
,
∴游戏对双方不公平;
修改得分规定为:若数字之积为3的倍数时,小亮得3分;若数字之积为5的倍数时,小丽得5分
【解析】(1)列表得出所有等可能的情况数,找出3的倍数与5的倍数,分别求出概率即可;(2)该游戏不公平,分别求出两人的得分,比较即可;修改规则使其概率相等即可.
【考点精析】利用列表法与树状图法对题目进行判断即可得到答案,需要熟知当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过调查获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:

(1)这次活动一共调查了名学生;
(2)补全条形统计图,并求出扇形统计图中选择篮球项目的人数所在扇形的圆心角的度数;
(3)若该学校有1200人,则该学校选择足球项目的学生人数约是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】某车间有60个工人,生产甲、乙两种零件,每人每天平均能生产甲种零件24个或乙种零件12个.已知每2个甲种零件和3个乙种零件配成一套,问应分配多少人生产甲种零件,多少人生产乙种零件,才能使每天生产的这两种零件刚好配套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=BC,△ABC≌△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点,观察并猜想线段EA1与FC有怎样的数量关系?并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=90°,∠AOC为∠AOB外的一个锐角,且∠AOC=30°,射线OM平分∠BOC,ON平分∠AOC.
(1)求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠AOC=β(β为锐角),其他条件不变,求∠MON的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:已知Q、K、R为数轴上三点,若点K到点Q的距离是点K到点R的距离的2倍,我们就称点K是有序点对
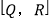 的好点.
的好点.根据下列题意解答问题:
(1)如图1,数轴上点Q表示的数为1,点P表示的数为0,点K表示的数为1,点R表示的数为2.因为点K到点Q的距离是2,点K到点R的距离是1,所以点K是有序点对
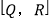 的好点,但点K不是有序点对
的好点,但点K不是有序点对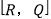 的好点.同理可以判断:点P是不是有序点对
的好点.同理可以判断:点P是不是有序点对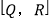 的好点;
的好点; (2)如图2,数轴上点M表示的数为-1,点N表示的数为5,点H表示的数为x,若点H是有序点对
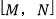 的好点,求x的值;
的好点,求x的值;(3)如图3,数轴上点A表示的数为20,点B表示的数为10.现有一只电子蚂蚁C从点B出发,以每秒3个单位的速度向左运动t秒(t>0).当点A、B、C中恰有一个点为其余两有序点对的好点,直接写出t的所有可能的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,已知点C在线段AB上,线段AC=6,BC=4,点M、N分别是AC、BC的中点,求MN的长度;
(2)根据(1)的计算过程与结果,设AC+BC=a,其它条件不变,请猜想出MN的长度吗?并说明理由;
(3)对于(1)题,如果将“点C在线段AB上”改为“点C在射线AB上”,其它条件不变,求MN的长度.

相关试题

