【题目】如图,在四边形ABCD中,给出了下列三个论断:①对角线AC平分∠BAD;②CD=BC;③∠D+∠B=180°.在上述三个论断中,若以其中两个论断作为条件,另外一个论断作为结论,则可以得出______个正确的命题.

参考答案:
【答案】3
【解析】
过点C作CE⊥AB,CF⊥AD,垂足为E、F,①②作为条件,可以证明△CBE与△CDF全等,根据全等三角形对应角相等可得∠B=∠CDF,再根据平角定义得到∠B+∠D=180°,所以③作为结论是正确的命题;①③作为条件,与前一种情况的思路相反,可以根据条件证明△CBE与△CDF全等,再根据全等三角形对应边相等得到CD=BC,所以②作为结论是正确的命题;②③作为条件,先证明∠B=∠CDF,再根据“角角边”证明△CBE与△CDF全等,根据全等三角形对应边相等可得CE=CF,再根据到角的两边距离相等的点在角的平分线上可得AC平分∠BAD,所以①作为结论是正确命题;
(1)共有:①②作为条件,③作为结论,
①③作为条件,②作为结论,
②③作为条件,①作为结论,3种情况,都是真命题,
故可以写出3个正确的命题;
故答案为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每次薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的是( )
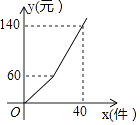
A.a=20
B.b=4
C.若工人甲一天获得薪金180元,则他共生产50件
D.若工人乙一天生产m(件),则他获得薪金4m元 -
科目: 来源: 题型:
查看答案和解析>>【题目】在2016年“双十一”期间,某快递公司计划租用甲、乙两种车辆快递货物,从货物量来计算:若租用两种车辆合运,10天可以完成任务;若单独租用乙种车辆,完成任务的天数是单独租用甲种车辆完成任务天数的2倍.
(1)求甲、乙两种车辆单独完成任务分别需要多少天?
(2)已知租用甲、乙两种车辆合运需租金65000元,甲种车辆每天的租金比乙种车辆每天的租金多1500元,试问:租甲和乙两种车辆、单独租甲种车辆、单独租乙种车辆这三种租车方案中,哪一种租金最少?请说明理由.
-
科目: 来源: 题型:
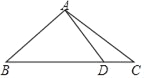
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,∠C=30°,AB⊥AD.
(1)求∠BDA的度数;
(2)若AD=2,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C 的圆心坐标为(0,﹣1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是( )
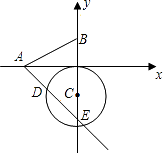
A.3
B.
C.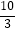
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=8,BC=5时,线段AE的长为____;
(2)若∠D=35°,∠C=60°,求∠DBC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点A、C对应的数分别为a、c,且a、c,满足|a+4|+(c﹣1)2018=0,点O对应的数为0,点B对应的数为﹣3.
(1)求数a、c的值;
(2)点A,B沿数轴同时出发向右匀速运动,点A速度为2个单位长度/秒,点B速度为1个单位长度/秒,几秒后,点A追上点B;
(3)在(2)的条件下,若运动时间为t秒,运动过程中,当A,B两点到原点O的距离相等时,求t的值.

相关试题

