【题目】某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)求甲种商品与乙种商品的销售单价;
(2)设销售甲种商品a万件.
① 甲、乙两种商品的销售总收入为 万元(用含a的代数式表示);
② 若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
参考答案:
【答案】(1)甲、乙两种商品的销售单价分别为900元,600元;(2)① (300a+4800);②至少销售甲种商品2万件.
【解析】
(1)设甲种商品的销售单价为x元,乙种商品的销售单价为y元.,根据题意列出二元一次方程组即可求解;
(2)①销售总收入的定义即可列出代数式;②根据题意列出不等式即可求解.
(1)设甲种商品的销售单价为x元,乙种商品的销售单价为y元.
根据题意,得![]()
解这个方程组,得![]()
答:甲、乙两种商品的销售单价分别为900元,600元.
(2)①销售甲种商品a万件,则销售乙种商品为(8-a)万件
∴甲、乙两种商品的销售总收入为900a+(8-a)×600=300a+4800,
故甲、乙两种商品的销售总收入为(300a+4800)万元
故答案为:(300a+4800);
② 根据题意,得300a+4800≥5400,解得a≥2.
答:至少销售甲种商品2万件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)

(1)数轴上点B对应的数是______.
(2)经过几秒,点M、点N分别到原点O的距离相等?
(3)当点M运动到什么位置时,恰好使AM=2BN?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的有( )
(1)、
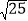 的平方根是±5;(2)、五边形的内角和是540°;(3)、抛物线y=x2+2x+4与x轴无交点;(4)、等腰三角形两边长为6cm和4cm,则它的周长是16cm.
的平方根是±5;(2)、五边形的内角和是540°;(3)、抛物线y=x2+2x+4与x轴无交点;(4)、等腰三角形两边长为6cm和4cm,则它的周长是16cm.A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】美丽的东昌湖赋于江北水城以灵性,周边景点密布。如图,A,B为湖滨的两个景点,C为湖心一个景点。景点B在景点C的正东,从景点
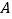 看,景点B在北偏东
看,景点B在北偏东 方向,景点C在北偏东
方向,景点C在北偏东 方向。一游客自景点A驾船以每分钟20米的速度行驶了10分钟到达景点C,之后又以同样的速度驶向景点B,该游客从景点C到景点B需用多长时间(精确到
方向。一游客自景点A驾船以每分钟20米的速度行驶了10分钟到达景点C,之后又以同样的速度驶向景点B,该游客从景点C到景点B需用多长时间(精确到 分钟)?
分钟)?(参考数据sin
 =0.97;cos
=0.97;cos =0.26,tan
=0.26,tan =3.73,
=3.73,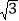 = 1.73)
= 1.73)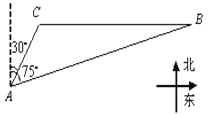
-
科目: 来源: 题型:
查看答案和解析>>【题目】东东在研究数学问题时遇到一个定义:将三个已经排好顺序数:x1,x2,x3,称为数列x1,x2,x3.计算|x1|,
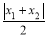 ,
,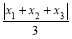 ,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,
,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,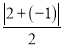 =
=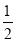 ,
, =
=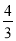 ,所以数列2,-1,3的最佳值为
,所以数列2,-1,3的最佳值为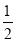 .
.东东进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列-1,2,3的最佳值为
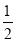 ;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为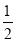 .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:(1)数列-4,-3,1的最佳值为
(2)将“-4,-3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
(3)将2,-9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的最佳值为1,求a的值.
-
科目: 来源: 题型:
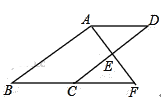
查看答案和解析>>【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB⊥AF,BC=12,EF=6,求CD的长.
相关试题

