【题目】如图,已知抛物线y=﹣ ![]() x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
(1)求抛物线的解析式及它的对称轴方程;
(2)求点C的坐标,连接AC、BC并求线段BC所在直线的解析式;
(3)试判断△AOC与△COB是否相似?并说明理由.
参考答案:
【答案】
(1)
解:∵抛物线y=﹣ ![]() x2+bx+4的图象经过点A(﹣2,0),
x2+bx+4的图象经过点A(﹣2,0),
∴﹣ ![]() ×(﹣2)2+b×(﹣2)+4=0,解得b=
×(﹣2)2+b×(﹣2)+4=0,解得b= ![]() ,
,
∴抛物线解析式为 y=﹣ ![]() x2+
x2+ ![]() x+4,
x+4,
又∵y=﹣ ![]() x2+
x2+ ![]() x+4=﹣
x+4=﹣ ![]() (x﹣3)2+
(x﹣3)2+ ![]() ,
,
∴对称轴方程为x=3
(2)
解:在y=﹣ ![]() x2+
x2+ ![]() x+4中,令x=0,得y=4,
x+4中,令x=0,得y=4,
∴C(0,4),
令y=0,即﹣ ![]() x2+
x2+ ![]() x+4=0,整理得x2﹣6x﹣16=0,解得x=8或x=﹣2,
x+4=0,整理得x2﹣6x﹣16=0,解得x=8或x=﹣2,
∴A(﹣2,0),B(8,0),
设直线BC的解析式为y=kx+b,
把B(8,0),C(0,4)的坐标分别代入解析式 ![]() ,解得
,解得  ,
,
∴直线BC的解析式为y=﹣ ![]() x+4
x+4
(3)
解:△AOC∽△COB成立.
理由如下:
在△AOC与△COD中,
∵OA=2,OC=4,OB=8,
∴ ![]() =
= ![]() ,
,
又∵∠AOC=∠BOC=90°,
∴△AOC∽△COB.

【解析】(1)把A点坐标代入抛物线解析式可求得b的值,则可求得抛物线解析式及其对称轴方程;(2)由抛物线解析式可求得A、B、C的坐标,根据待定系数法可求得直线BC的解析式;(3)由A、B、C的坐标可求得OA、OC、OB的长,根据相似三角形的判定可证明△AOC∽△COB.
【考点精析】掌握二次函数的图象和二次函数的性质是解答本题的根本,需要知道二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E分别在BC、AB上,且∠BDE=∠CAD.求证:△ADE∽△ABD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x﹣1与反比例函数y=
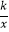 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m). 
(1)求反比例函数的解析式;
(2)若点P(n,﹣1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖.

(1)如果操场上铺灰色地面砖的面积是铺红色地面砖面积的4倍,那么操场四角的每个小正方形边长是多少米?
(2)如果灰色地面砖的价格为每平方米30元,红色地面砖的价格为每平方米20元,学校现有15万元资金,问这些资金是否能购买所需的全部地面砖?如果能购买所学的全部地面砖,则剩余资金是多少元?如果不能购买所需的全部地面砖,教育局还应该至少给学校解决多少资金? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为13,弦AB∥CD,AB=24,CD=10,则AB、CD之间的距离为( )
A.17
B.7
C.12
D.7或17 -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax2+bx与y=ax+b的图象可能是( )
A.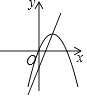
B.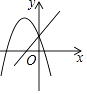
C.
D.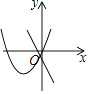
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )

A.(2,5)
B.(5,2)
C.(4, )
)
D.( ,4)
,4)
相关试题

