【题目】在同一平面直角坐标系中，函数y=ax2+bx与y=ax+b的图象可能是（ ）
A.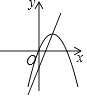
B.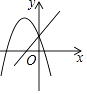
C.
D.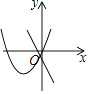

参考答案：

【答案】C
【解析】解：二次函数的对称轴为：x=﹣ 当a＞0，b＞0时，
一次函数的图象经过一、二、三象限，
二次函数的图象开口向上，对称轴x＜0，
当a＞0，b＜0时，
一次函数的图象经过一、三、四象限，
二次函数的图象开口向上，对称轴x＞0，
当a＜0，b＞0时，
一次函数的图象经过一、二、四象限，
二次函数的图象开口向下，对称轴x＞0，
当a＜0，b＜0时，
一次函数的图象经过二、三、四象限，
二次函数的图象开口向下，对称轴x＜0，
故选C
【考点精析】通过灵活运用一次函数的图象和性质和二次函数的图象，掌握一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远；二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点即可以解答此题．

关闭