【题目】如图,已知![]() ,
,![]() ,
,![]() .试说明直线
.试说明直线![]() 与
与![]() 垂直.(请在下面的解答过程的空格内填空或在括号内填写理由).
垂直.(请在下面的解答过程的空格内填空或在括号内填写理由).

理由:![]() ,(已知)
,(已知)
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
又![]() ,(已知)
,(已知)
![]()
![]() .(等量代换)
.(等量代换)
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]() ,(已知)
,(已知)
![]() ,
,![]() ,
,
![]()
![]() .
.
参考答案:
【答案】GD,AC,同位角相等,两直线平行;∠DAC,两直线平行,内错角相等;∠DAC;AD,EF,同旁内角互补,两直线平行;两直线平行,同位角相等;AD,BC.
【解析】
结合图形,根据平行线的判定和性质逐一进行填空即可.
∵∠1=∠C,(已知)
∴GD∥AC,(同位角相等,两直线平行)
∴∠2=∠DAC.(两直线平行,内错角相等)
又∵∠2+∠3=180°,(已知)
∴∠3+∠DAC=180°.(等量代换)
∴AD∥EF,(同旁内角互补,两直线平行)
∴∠ADC=∠EFC.(两直线平行,同位角相等)
∵EF⊥BC,(已知 )
∴∠EFC=90°,
∴∠ADC=90°,
∴AD⊥BC.
故答案为:GD,AC,同位角相等,两直线平行;∠DAC,两直线平行,内错角相等;∠DAC;AD,EF,同旁内角互补,两直线平行;两直线平行,同位角相等;AD,BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小刚身高180cm,他站立在阳光下的影子长为90cm,他把手臂竖直举起,此时影子长为115cm,那么小刚的手臂超出头顶cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1为北京城市女生从出生到15岁的平均身高统计图,图2是北京城市某女生从出生到12岁的身高统计图.

请你根据以上信息预测该女生15岁时的身高约为 , 你的预测理由是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于双曲线y=
 (m>0)和双曲线y=
(m>0)和双曲线y= 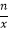 (n>0),如果m=2n,则称双曲线y=
(n>0),如果m=2n,则称双曲线y=  (m>0)和双曲线y=
(m>0)和双曲线y= 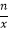 (n>0)为“倍半双曲线”,双曲线y=
(n>0)为“倍半双曲线”,双曲线y=  (m>0)是双曲线y=
(m>0)是双曲线y= 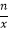 (n>0)的“倍双曲线”,双曲线y=
(n>0)的“倍双曲线”,双曲线y= 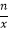 (n>0)是双曲线y=
(n>0)是双曲线y=  (m>0)的“半双曲线”,
(m>0)的“半双曲线”,
(1)请你写出双曲线y=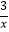 的“倍双曲线”是;双曲线y=
的“倍双曲线”是;双曲线y= 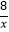 的“半双曲线”是;
的“半双曲线”是;
(2)如图1,在平面直角坐标系xOy中,已知点A是双曲线y=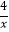 在第一象限内任意一点,过点A与y轴平行的直线交双曲线y=
在第一象限内任意一点,过点A与y轴平行的直线交双曲线y= 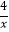 的“半双曲线”于点B,求△AOB的面积;
的“半双曲线”于点B,求△AOB的面积;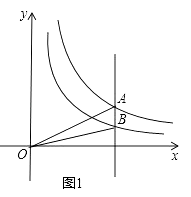
(3)如图2,已知点M是双曲线y=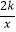 (k>0)在第一象限内任意一点,过点M与y轴平行的直线交双曲线y=
(k>0)在第一象限内任意一点,过点M与y轴平行的直线交双曲线y= 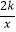 的“半双曲线”于点N,过点M与x轴平行的直线交双曲线y=
的“半双曲线”于点N,过点M与x轴平行的直线交双曲线y= 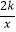 的“半双曲线”于点P,若△MNP的面积记为S△MNP , 且1≤S△MNP≤2,求k的取值范围.
的“半双曲线”于点P,若△MNP的面积记为S△MNP , 且1≤S△MNP≤2,求k的取值范围.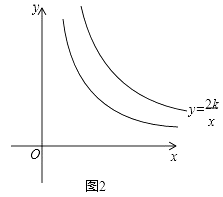
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数
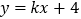 的图象经过点(-3,-2).
的图象经过点(-3,-2).(1)求这个函数表达式;
(2)判断(-5,3)是否在这个函数的图象上.
(3)点M在直线y=kx+4上且到y轴的距离是3,求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF.
(1)求证:∠DAF=∠F;
(2)在不添加任何辅助线的情况下,请直接写出所有与∠CED互余的角.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD和正方形DEFG中,顶点B、D、F在同一直线上,H是BF的中点.
(1)如图1,若AB=1,DG=2,求BH的长;
(2)如图2,连接AH,GH.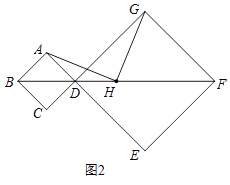
小宇观察图2,提出猜想:AH=GH,AH⊥GH.小宇把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:延长AH交EF于点M,连接AG,GM,要证明结论成立只需证△GAM是等腰直角三角形;
想法2:连接AC,GE分别交BF于点M,N,要证明结论成立只需证△AMH≌△HNG.
…
请你参考上面的想法,帮助小宇证明AH=GH,AH⊥GH.(一种方法即可)
相关试题

