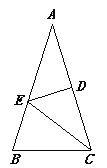
【题目】如图19,在△ABC中,AB=AC,AC的垂直平分线交AB于E,D为垂足,连接EC.若BC=EC,求∠BED的度数.
参考答案:
【答案】126°.
【解析】试题分析:
由DE垂直平分AC可得AE=CE=BC,由此可得∠A=∠ECA,∠CEB=∠ABC;由AB=AC可得∠ABC=∠ACB,又因为∠CEB=∠A+∠ECA=2∠A,所以∠ABC=∠ACB=2∠A,再由三角形内角和为180°,在△ABC中可解得∠A的度数,最后由∠BED=∠A+∠EDC可求得∠BED的度数.
试题解析:
∵DE垂直平分AC,
∴AE=CE,∠ADE=90°.
∴∠A=∠ACE.
∵AB=AC,BC=EC,
∴∠ACB=∠B=∠BEC.
设∠A=x,则∠BEC=∠A+∠ACE=2x.
∴∠ACB=∠B=∠BEC=2x.
∴∠A+∠B+∠ACB=x+2x+2x=180°.
解得x=36°.
∴∠BED=∠A+∠ADE=36°+90°=126°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据测算,1粒芝麻重0.000004克,数0.000004可用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为每件50元,售价为每件60元,每个月可卖出200件;如果每件商品的售价每上涨1元.则每个月少卖10件.设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)若每个月的利润不低于2160元,售价应在什么范围?
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形三条中线的交点叫做三角形的
A. 内心 B. 外心 C. 中心 D. 重心
-
科目: 来源: 题型:
查看答案和解析>>【题目】若2(a+3)的值与4互为相反数,则a值为________
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只电子蚂蚁在数轴上从-3出发向左运动2个单位长度到点A处,再向右运动4个单位长度到点C处.
(1)画出数轴标出A、C所表示的数;
(2)这只电子蚂蚁一共运动多少个单位长度? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图.A、B、C三点在数轴上,A表示的数为-10,B表示的数为14,点C在点A与点B之间,且AC=BC.
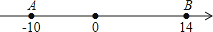
(1)求A、B两点间的距离;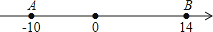
(2)求C点对应的数;
(3)甲、乙分别从A、B两点同时相向运动,甲的速度是1个单位长度/s,乙的速度是2个单位长度/s,求相遇点D对应的数.
相关试题

