【题目】如图22,在∠AOB的两边OA,OB上分别取OM=ON,OD=OE,DN和EM相交于点C.求证:点C在∠AOB的平分线上.
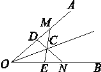
参考答案:
【答案】见解析
【解析】
过点C分别作CG⊥OA于点G,CF⊥OB于点F,在△MOE和△NOD中,根据OM=ON,∠MOE=∠NOD,OE=OD,可判定△MOE≌△NOD,根据全等三角形的性质可得:S△MOE=S△NOD,继而可得S△MOE-S四边形ODCE=S△NOD-S四边形ODCE,即S△MDC=S△NEC.
由三角形面积公式得DM·CG=EN·CF.由于OM=ON,OD=OE,所以DM=EN,CG=CF.
根据CG⊥OA,CF⊥OB,可证点C在∠AOB的平分线上.
证明:过点C分别作CG⊥OA于点G,CF⊥OB于点F,
如图.

在△MOE和△NOD中,OM=ON,∠MOE=∠NOD,OE=OD,
∴△MOE≌△NOD(SAS),
∴S△MOE=S△NOD,
∴S△MOE-S四边形ODCE=S△NOD-S四边形ODCE,
即S△MDC=S△NEC.
由三角形面积公式得DM·CG=EN·CF.
∵OM=ON,OD=OE,
∴DM=EN,
∴CG=CF.
又∵CG⊥OA,CF⊥OB,
∴点C在∠AOB的平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c与x轴交于点A,B(A在B的左侧),抛物线的对称轴为直线x=1,AB=4.

(1)求抛物线的表达式;
(2)抛物线上有两点M(x1 , y1)和N(x2 , y2),若x1<1,x2>1,x1+x2>2,试判断y1与y2的大小,并说明理由;
(3)直线l过A及C(0,﹣2),P为抛物线上一点(在x轴上方),过P作PD∥y轴交直线AC于点D,以PD为直径作⊙E,求⊙E在直线AC上截得的线段的最大长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两点在数轴上对应的数分别为a,b,且点A在点B的左边,|a|=10,a+b=80,ab<0.
(1)求出a,b的值;
(2)现有一只电子蚂蚁P从点A出发,以3个单位长度/秒的速度向右运动,同时另一只电子蚂蚁Q从点B出发,以2个单位长度/秒的速度向左运动.
①设两只电子蚂蚁在数轴上的点C相遇,求出点C对应的数是多少?
②经过多长时间两只电子蚂蚁在数轴上相距20个单位长度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,反比例函数y=
 (x>0)的图象经过A、B两点,菱形ABCD在第一象限内,边BC于x轴平行.若A、B两点的纵坐标分别为3和1,则菱形ABCD的面积为( )
(x>0)的图象经过A、B两点,菱形ABCD在第一象限内,边BC于x轴平行.若A、B两点的纵坐标分别为3和1,则菱形ABCD的面积为( ) 
A.2
B.4
C.2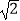
D.4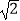
-
科目: 来源: 题型:
查看答案和解析>>【题目】结合数轴与绝对值的知识回答下列问题:
数轴上表示4和1的两点之间的距离是3:而|4-1|=3;表示-3和2两点之间的距离是5:而|-3-2|=5;表示-4和-7两点之间的距离是3,而|-4-(-7)|=3.
一般地,数轴上表示数m和数n的两点之间的距离公式为|m-n|.
(1)数轴上表示数-5的点与表示-2的点之间的距离为______;
(2)数轴上表示数a的点与表示-4的点之间的距离表示为______;若数轴上a位于-4与2之间,求|a+4|+|a-2|的值;
(3)如果表示数a和3的两点之间的距离是7,则可记为:|a-3|=7,求a的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,按如下步骤作图: ①分别以点B、C为圆心,大于
 AB的长为半径作弧,两弧相交于点M和N;
AB的长为半径作弧,两弧相交于点M和N;
②作直线MN交AC于点D,
③连接BD,
若AC=8,则BD的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形ABCD的三个顶点A、B、D均在抛物线y=ax2﹣4ax+3(a<0)上.若点A是抛物线的顶点,点B是抛物线与y轴的交点,则AC长为 .
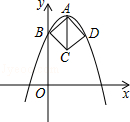
相关试题

