Question

【题目】如图，AB是⊙O的弦，OC⊥AB于点C，连接OA，AB=12，⊙O半径为10．

（1）求OC的长；

（2）点E，F在⊙O上，EF∥AB．若EF=16，直接写出EF与AB之间的距离．

Answer 1

【答案】（1）8; （2）2或14．

【解析】

试题分析：（1）由垂径定理求得AC=6；然后通过解Rt△AOC来求OC的长度；

（2）需要分类讨论：EF在圆心是下方和EF在圆心的上方两种情况．

试题解析：（1）∵AB是⊙O的弦，OC⊥AB于C，AB=12，

∴AC=AB=6．

∵在Rt△AOC中，∠ACO=90°，cosA=，

∴OA=10，

∴OC==8；

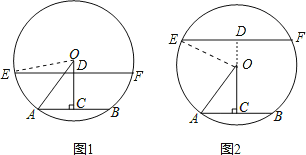
（2）设直线CO交EF于点D，连接OE．

∵EF∥AB，

∴OD⊥EF，ED=EF=8．

∴在直角△OED中，根据勾股定理得到：OD=

如图1，CD=OC-OD=8-6=2；

如图2，CD=OC，+OD=8+6=14；

综上所述，EF与AB之间的距离是2或14．