【题目】如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;

(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
参考答案:
【答案】(1)抛物线的解析式为y=﹣x2+3x+4.(2)点P的坐标为(2,6)或(4,0).(3)△PBC的面积的最大值为8.
【解析】试题分析:(1)将点A(-1,0),B(4,0)的坐标代入抛物线的解析式,求得b、c的值即可;
(2)先由函数解析式求得点C的坐标,从而得到△OBC为等腰直角三角形,故此当CF=PF时,以P,C,F为顶点的三角形与△OBC相似.
设点P的坐标为(a,-a2+3a+4).则CF=a,PF=-a2+3a,接下来列出关于a的方程,从而可求得a的值,于是可求得点P的坐标;
(3)连接EC.设点P的坐标为(a,-a2+3a+4).则OE=a,PE=-a2+3a+4,EB=4-a.然后依据S△PBC=S四边形PCEB-S△CEB列出△PBC的面积与a的函数关系式,从而可求得三角形的最大面积.
试题解析:(1)将点A(-1,0),B(4,0)的坐标代入函数的表达式得:
![]() ,
,
解得:b=3,c=4.
抛物线的解析式为y=-x2+3x+4.
(2)如图1所示:
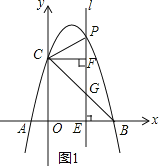
∵令x=0得y=4,
∴OC=4.
∴OC=OB.
∵∠CFP=∠COB=90°,
∴FC=PF时,以P,C,F为顶点的三角形与△OBC相似.
设点P的坐标为(a,-a2+3a+4)(a>0).
则CF=a,PF=|-a2+3a+4-4|=|a2-3a|.
∴|a2-3a|=a.
解得:a=2,a=4.
∴点P的坐标为(2,6)或(4,0).
(3)如图2所示:连接EC.
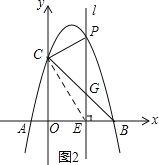
设点P的坐标为(a,-a2+3a+4).则OE=a,PE=-a2+3a+4,EB=4-a.
∵S四边形PCEB=![]() OBPE=
OBPE=![]() ×4(-a2+3a+4),S△CEB=
×4(-a2+3a+4),S△CEB=![]() EBOC=
EBOC=![]() ×4×(4-a),
×4×(4-a),
∴S△PBC=S四边形PCEB-S△CEB=2(-a2+3a+4)-2(4-a)=-2a2+8a.
∵a=-2<0,
∴当a=2时,△PBC的面积S有最大值.
∴P(2,6),△PBC的面积的最大值为8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一些笔记本分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人就分不到3本,但至少有1本.则共有学生( )
A. 4人 B. 5人
C. 6人 D. 5人或6人
-
科目: 来源: 题型:
查看答案和解析>>【题目】三个连续正整数的和小于39,这样的正整数中,最大一组的和是( )
A.39
B.36
C.35
D.34 -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校把学生的期中测试、期末测试两项成绩分别按40%,60%的比例计入学期总成绩,小明的期中测试成绩为81分,若他的学期总成绩不低于90分,则小明的期末测试成绩至少是________分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】课堂练习中,王莉同学做了如下4道因式分解题,你认为王莉做得不够完整的一道是( )
A. x3-x=x(x2-1)
B. x2+2xy+y2=(x+y)2
C. x2y-xy2=xy(x-y)
D. ab2-6ab+9a=a(b-3)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.
(1)求证:∠FBC=∠FCB;
(2)已知FAFD=12,若AB是△ABC外接圆的直径,FA=2,求CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干、小分支的总数为133,则每个支干长出___________个小分支
相关试题

