【题目】某中学开展“阳光体育一小时”活动,根据学校实际情况,决定开设A:踢毽子;B:篮球:C:跳绳;D:乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如两个统计图.请结合图中的信息解答下列问题:
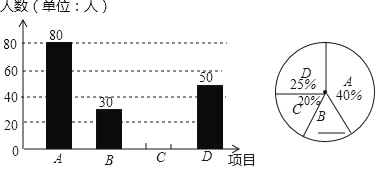
(1)本次共调查了多少名学生?
(2)请将两个统计图补充完整.
(3)求图中“A”层次所在扇形的圆心角的度数.
参考答案:
【答案】(1)200名学生;(2)见解析;(3)144°.
【解析】
(1)结合条形统计图和扇形统计图,利用A组频数80除以A组频率40%,即可得到该校本次调查中,共调查了多少名学生;
(2)利用(1)中所求人数,减去A、B、D组的频数即可的C组的频数;B组频数除以总人数即可得到B组频率;
(3)用360°乘以A对应的百分比可得.
(1)80÷40%=200(人)
故本次共调查200名学生.
(2)200﹣80﹣30﹣50=40(人),
30÷200×100%=15%,
补全如图:
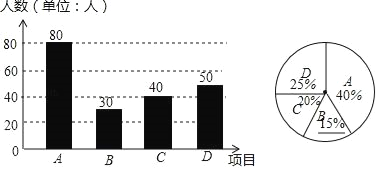
(3)图中“A”层次所在扇形的圆心角的度数为360°×40%=144°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线AB∥CD,直线EF与AB,CD分别相交于点E,F.
(1)如图1,若∠1=60°,求∠2,∠3的度数.

(2)若点P是平面内的一个动点,连结PE,PF,探索∠EPF,∠PEB,∠PFD三个角之间的关系.
①当点P在图(2)的位置时,可得∠EPF=∠PEB+∠PFD请阅读下面的解答过程并填空(理由或数学式)
解:如图2,过点P作MN∥AB
则∠EPM=∠PEB(_______)
∵AB∥CD(已知)MN∥AB(作图)
∴MN∥CD(_______)
∴∠MPF=∠PFD (_______)
∴_____=∠PEB+∠PFD(等式的性质)
即:∠EPF=∠PEB+∠PFD
②拓展应用,当点P在图3的位置时,此时∠EPF=80°,∠PEB=156°,则∠PFD=_____度.
③当点P在图4的位置时,请直接写出∠EPF,∠PEB,∠PFD三个角之间关系_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 +(﹣1)2017+(3.14﹣π)﹣(﹣
+(﹣1)2017+(3.14﹣π)﹣(﹣  )﹣2 .
)﹣2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】作为武汉市政府民生实事之一的公共自行车建设工作已基本完成,“摩拜单车”等租车服务进入市民的生活.某部门对今年5月份一周中的连续7天进行了公共自行车日租车量的统计,并绘制了如下条形图:
(1) 求这7天日租车量的众数与中位数;
(2) 求这7天日租车量的平均数,并用这个平均数估计5月份(31天)共租车多少万车次?

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两车间共120人,其中甲车间人数比乙车间人数的4倍少5人.
(1)求甲、乙两车间各有多少人?
(2)若从甲、乙两车间分别抽调工人,组成丙车间研制新产品,并使甲、乙、丙三个车间的人数比为13∶4∶7,那么甲、乙两车间要分别抽调多少工人?
-
科目: 来源: 题型:
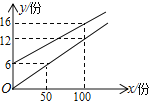
查看答案和解析>>【题目】武汉市某校实行学案式教学,需印制若干份数学学案.印刷厂有甲、乙两种收费方式,除按印刷份数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示
(1) 求甲、乙两种收费方式的函数关系式;
(2) 当印刷多少份学案时,两种印刷方式收费一样?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD中,AB=8,第一次平移长方形ABCD沿AB的方向向右平移6个单位,得到长方形A1B1C1D1,第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移6个单位,得到长方形A2B2C2D2,……第n次平移将长方形An﹣1Bn﹣1 Cn﹣1 Dn﹣1 的方向平移6个单位,得到长方形AnBnCnDn(n>2),若ABn的长度为2018,则n的值为( )

A. 334 B. 335 C. 336 D. 337
相关试题

