Question

【题目】如图在平面直角坐标系xoy中，直线y＝2x+4与y轴交于A点，与x轴交于B点，抛物线C1：y=－x＋bx+c过A、B两点，与x轴另一交点为C。

（1）（3分）求抛物线解析式及C点坐标。

（2）（4分）向右平移抛物线C1，使平移后的抛物线C2恰好经过△ABC的外心，抛物线C1、C2相交于点D，求四边形AOCD的面积。

（3）（5分）已知抛物线C2的顶点为M，设P为抛物线C1对称轴上一点，Q为抛物线C1上一点，是否存在以点M、Q、P、B为顶点的四边形为平行四边形，若存在，直接写出P点坐标，不存在，请说明理由。

图（1） 图（2）

Answer 1

【答案】(1) y=－ x＋x＋4，C(8，0)；（2）；（3）存在，点P的坐标为（3，0）或(3，-）或(3，-25））.

【解析】

试题分析：（1）在y＝2x+4中，令x=0，可得y=4，则点A的坐标为A(0，4)；令y=0，可得x=－2，则点B的坐标为(－2，0)；因为抛物线C1：y=－x＋bx+c过A、B两点，故将A(0，4)，B(－2，0)代入y=－x＋bx+c，联立方程组，求解b，c的值即可求得抛物线解析式y=－ x＋x＋4，再令－ x＋x＋4=0，即可得C点坐标；（2）先证明△ABC是直角三角形，得△ABC的斜边BC的中点为(3，0)即E点坐标为(3,0) ，由平移可得F点坐标为F (13，0)，从而得出抛物线C的解析式，再将C1、C联立方程组解出x，y的值，最后根据S四边形AOCD= S三角形AOD＋S三角形 OCD即可得出四边形AOCD的面积；（3）分情况讨论可能的情形即可得出结论.

试题解析： ⑴∵直线y＝2x+4与y轴交于A点，与x轴交于B点，

∴令x=0，可得y=4，则点A的坐标为A(0，4)；

令y=0，可得x=－2，则点B的坐标为(－2，0)；

将A(0，4)，B(－2，0)代入y=－x＋bx+c，联立方程组，

解得，b=, c=4

∴抛物线C的解析式为: y=－ x＋x＋4

∵抛物线C1：y=－x＋bx+c与x轴交于点C

令－ x＋x＋4=0，

解得，x=8

∴C点坐标为C(8，0)

⑵如图，

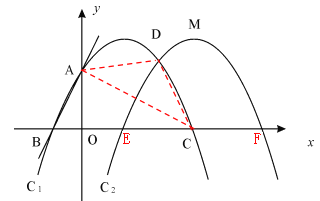
由（1）知，C(8，0)，A(0，4)，B (－2，0)

∴AC2=AO2+OC2=42+82=80，

AB2= AO2+OB2=42+22=20，

又BC=BO+OC=8+2=10，∴BC2= 102=100

∴BC2= AC2+AB2，

∴△ABC是直角三角形.

△ABC的斜边BC的中点为(8+2)÷2=5

∴OE=5-OB=5-2=3

∴△ABC的斜边BC的中点为(3,0)

∵抛物线C2恰好经过△ABC的外心，

∴ E为△ABC的外心，E点坐标为(3,0)

∴F点坐标为(3+8+2，0)，即F(13，0)

由E (3,0) ，F(13，0)得抛物线C∶y= - (x-3 ) (x-13 )

即C∶y= -x＋4x－

联立方程组

解得 x= y=

∴S四边形AOCD= S三角形AOD＋S三角形 OCD

＝×4×＋×8×=

答：四边形AOCD的面积为.

⑶分情况讨论如下：

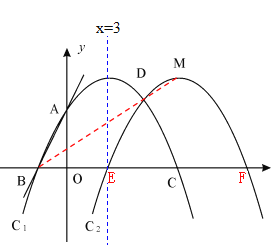
①BM为对角线时，中点在直线x=3上，Q（3，）

所以P（3，0）

②当四边形PQBM为平行四边形时PQ∥MB， Q（-7，-）,

所以P(3，-）

③当四边形PQMB为平行四边形时PQ∥BM，Q（13，-）,

所以P(3，-25）