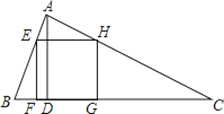
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长.
参考答案:
【答案】(1)证明见解析;(2)![]() cm.
cm.
【解析】试题分析:(1)根据EH∥BC即可证明.
(2)如图设AD与EH交于点M,首先证明四边形EFDM是矩形,设正方形边长为x,再利用△AEH∽△ABC,得![]() ,列出方程即可解决问题.
,列出方程即可解决问题.
试题解析:(1)证明:∵四边形EFGH是正方形,
∴EH∥BC,
∴∠AEH=∠B,∠AHE=∠C,
∴△AEH∽△ABC.
(2)∵∠EFD=∠FEO=∠FDO=90°,
∴四边形EFDO是矩形,
∴EF=DO,设正方形EFGH的边长为x,
∵△AEH∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴x=![]() ,
,
∴正方形EFGH的边长为![]() cm.
cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为使我市冬季“天更蓝、房更暖”、政府决定实施“煤改气”供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中:
①甲队每天挖100米; ②乙队开挖两天后,每天挖50米;
③当x=4时,甲、乙两队所挖管道长度相同; ④甲队比乙队提前2天完成任务.正确的个数有( )
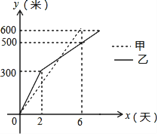
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10,…这样的数称为“三角形数”,而把1,4,9,16,…这样的数称为“正方形数”.
(1)第5个“三角形数”是 ,第n个“三角形数”是 ,第5个“正方形数”是 ,第n个“正方形数”是 .
(2)除“1”以外,请再写一个既是“三角形数”,又是“正方形数”的数 .
(3)经探究我们发现:任何一个大于1的“正方形数”都可以看做两个相邻“三角形数”之和. 例如:①4=1+3;②9=3+6;③16=6+10;④ ;⑤ ;…请写出上面第4个和第5个等式.
(4)在(3)中,请探究n2= + 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句正确的是( )
A. 1+a不是一个代数式 B. 0是代数式
C. S=πr2是一个代数式 D. 单独一个字母a不是代数式
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC≌△DEF,AB=2,AC=4,若△DEF的周长为偶数,则EF的取值为( )
A.3
B.4
C.5
D.3或4或5 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 三点确定一个圆
B. 长度相等的弧是等弧
C. 任意一个三角形只有一个外接圆
D. 三角形的外心到三角形的三边距离相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一边长是8cm,另一边长是5cm,则它的周长是__________cm.
相关试题

