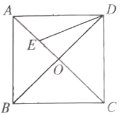
【题目】如图,正方形ABCD的对角线AC,BD交于点O,DE平分![]() 交OA于点E,若
交OA于点E,若![]() ,则线段OE的长为________.
,则线段OE的长为________.
参考答案:
【答案】2-![]()
【解析】
由正方形的性质可得AB=CD,∠COD=90°,OC=OD,∠ADB=∠ACD=∠CDO=45°,又因DE平分∠ODA,所以∠BDE=∠ADE=22.5°;在△ADE中,根据三角形的内角和定理可得∠CED=67.5°,所以∠CED=∠CDE=67.5°;根据等腰三角形的性质可得CD=CE=2;在等腰Rt△COD中,根据勾股定理求得OC=![]() ,由此即可求得OE的长.
,由此即可求得OE的长.
∵四边形ABCD为正方形,
∴AB=CD,∠COD=90°,OC=OD,∠ADB=∠ACD=∠CDO=45°,
∵DE平分![]() ,
,
∴∠BDE=∠ADE=22.5°,
∴∠CDE=∠BDE+∠CDO =67.5°;
在△ADE中,根据三角形的内角和定理可得∠CED=67.5°,
∴∠CED=∠CDE=67.5°,
∴CD=CE=2,
在等腰Rt△COD中,根据勾股定理求得OC=![]() ,
,
∴OE=CE-OC=2-![]() .
.
故答案为:2-![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.
(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?
-
科目: 来源: 题型:
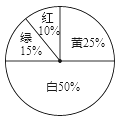
查看答案和解析>>【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘(如下图),并规定:购买100元的商品,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、绿、黄、白区域,那么顾客就可以分别得到80元、30元、10元、0元的购物券,凭购物券仍然可以在商场购物;如果顾客不愿意转转盘,那么可以直接获得购物券10元.
(1)每转动一次转盘所获购物券金额的平均数是多少?
(2)若在此商场购买100元的货物,那么你将选择哪种方式获得购物券?
(3)小明在家里也做了一个同样的转盘做实验,转10次后共获得购物券96元,他说还是不转转盘直接领取购物券合算,你同意小明的说法吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两根木条,一根长60cm,一根长100cm,将它们的一个端点重合,放在同一条直线上,此时两根木条中点间的距离( )
A.20cmB.80cm
C.160cmD.20cm 或80cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由;
(4)你能用一句简洁的话,描述你发现的结论吗?
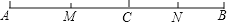
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的抛物线是二次函数
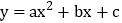 (a≠0)的图象,则下列结论:①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b;⑤3a+c<0.其中正确的结论有
(a≠0)的图象,则下列结论:①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b;⑤3a+c<0.其中正确的结论有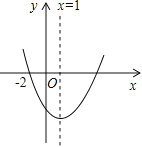
A. 5个 B. 4个 C. 3个 D. 2个
相关试题

