【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将一个含30°的直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(图中∠OMN=30°,∠NOM=90°)
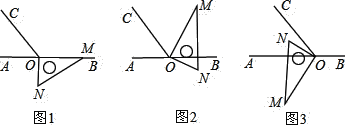
(1)将图1中的三角板绕点O逆时针旋转至图2,使OM在∠BOC的内部,且恰好平分∠BOC,问直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,求t;
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
参考答案:
【答案】(1)直线ON平分∠AOC,理由详见解析;(2)t=10或t=40;(3)∠AOM–∠NOC=30°.
【解析】
(1)由角的平分线的定义和等角的余角相等求解;
(2)由∠BOC=120°可得∠AOC=60°,则∠AON=30°或∠NOR=30°,即顺时针旋转300°或120°时ON平分∠AOC,据此求解;
(3)因为∠MON=90°,∠AOC=60°,所以∠AOM=90°-∠AON、∠NOC=60°-∠AON,然后作差即可.
解:(1)直线ON平分∠AOC;
理由:
设ON的反向延长线为OD,
∵OM平分∠BOC,
∴∠MOC=∠MOB=60°,
又∵OM⊥ON,
∴∠MON=90°,
∴∠BON=30°,
∴∠CON=120°+30°=150°,
∴∠COD=30°,
∴OD平分∠AOC,
即直线ON平分∠AOC;
(2)由(1)可知∠BON=30°,∠DON=180°,
因此ON旋转60°或240°时直线ON平分∠AOC,
由题意得,6t=60°或240°,
∴t=10或40;
(3)∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°-∠AON、∠NOC=60°-∠AON,
∴∠AOM-∠NOC=(90°-∠AON)-(60°-∠AON)=30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A.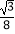
B.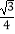
C.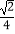
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为()

A.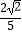
B.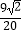
C.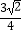
D.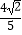
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2﹣bx﹣2(a≠0)的图象的顶点在第四象限,且过点(﹣1,0),当a﹣b为整数时,ab的值为( )
A. 或1
或1
B. 或1
或1
C. 或
或 
D. 或
或 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,B,C两点把线段AD分成4:5:7的三部分,E是线段AD的中点,CD=14厘米.
(1)求EC的长.
(2)求AB:BE的值.
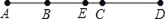
-
科目: 来源: 题型:
查看答案和解析>>【题目】设一次函数y=kx+2k-3(k≠0),对于任意两个k的值k1,k2,分别对应两个一次函数值y1,y2,若k1k2<0,当x=m时,取相应y1,y2,中的较小值p,则p的最大值是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据图中提供的信息,回答下列问题

(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定: 这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
相关试题

