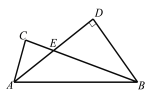
【题目】如图,在![]() 中, AD平分∠CAB交BC于点E. 若∠BDA=90°,E是AD中点,DE=2,AB=5,则AC的长为( )
中, AD平分∠CAB交BC于点E. 若∠BDA=90°,E是AD中点,DE=2,AB=5,则AC的长为( )
A.1B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】D
【解析】
过点C作CF⊥AD于F,易求AE=2,AD=4,BD=![]() =3由角平分线性质得出∠CAF=∠DAB,由tan∠DAB=
=3由角平分线性质得出∠CAF=∠DAB,由tan∠DAB=![]() ,推出
,推出![]() ,则AF=
,则AF=![]() ,由tan∠BED=
,由tan∠BED=![]() ,∠CEF=∠BED,得出
,∠CEF=∠BED,得出![]() 则EF=
则EF=![]() ,由AF+EF=AE=2,求出CF=1,AF=
,由AF+EF=AE=2,求出CF=1,AF=![]() ,则AC=
,则AC=![]() .
.
解:过点C作CF⊥AD于F,如图所示:
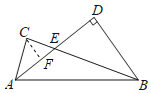
∵E是AD中点,DE=2,
∴AE=2,AD=4,BD=![]() =3
=3
∵AD平分∠CAB,
∴∠CAF=∠DAB,
∵tan∠DAB=![]()
∴![]()
∴AF=![]()
∵tan∠BED=![]() ,∠CEF=∠BED,
,∠CEF=∠BED,
∴![]() 则EF=
则EF=![]() ,
,
∵AF+EF=AE=2,
![]()
∴CF=1,AF=![]() ,
,
∴AC=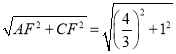 =
=![]() .
.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:
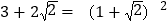 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:设
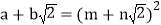 (其中
(其中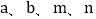 均为整数),则有
均为整数),则有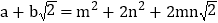 .
.∴
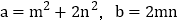 .这样小明就找到了一种把部分
.这样小明就找到了一种把部分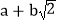 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
当
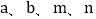 均为正整数时,若
均为正整数时,若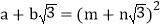 ,用含m、n的式子分别表示
,用含m、n的式子分别表示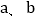 ,得
,得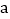 = ,
= ,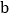 = ;
= ;(2)利用所探索的结论,找一组正整数
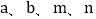 ,填空: + =( +
,填空: + =( + 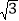 )2;
)2;(3)若
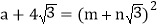 ,且
,且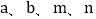 均为正整数,求
均为正整数,求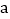 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具店进了一排黑白塑料球,共5箱,每箱的规格、数量都相同,其中每箱中装有黑白两种颜色的塑料球共3000个,为了估计每箱中两种颜色球的个数,随机抽查了一箱,将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,发现摸到黑球的概率在0.8附近波动,则此可以估计这批塑料球中黑球的总个数,请将黑球总个数用科学记数法表示约为________个.
-
科目: 来源: 题型:
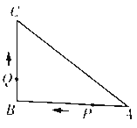
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,AB=8 cm,BC=6 cm,P,Q是△ABC边上的两个动点,点P从点A开始沿A→B方向运动,且速度为1 cm,点Q从点B开始沿B→C方向运动,且速度为2 cm/s,它们同时出发,设运动的时间为t s.
(1)运动几秒时,△APC是等腰三角形?
(2)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】凸四边形ABCD的两条对角线和两条边的长度都为1,则四边形ABCD中最大内角度数为( )
A.150°B.135°C.120°D.105°
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程
(1)x2﹣4x+1=0 (2)(5x﹣3)2+2(3﹣5x)=0
(3)(2x+1)2=(x﹣1)2 (4)4x2+2=7x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B.
(1)求证:AD是⊙O的切线.
(2)若BC=8,tanB=
 ,求⊙O的半径.
,求⊙O的半径.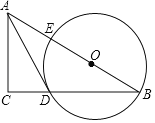
相关试题

