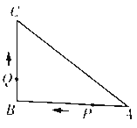
【题目】如图,已知△ABC中,∠B=90°,AB=8 cm,BC=6 cm,P,Q是△ABC边上的两个动点,点P从点A开始沿A→B方向运动,且速度为1 cm,点Q从点B开始沿B→C方向运动,且速度为2 cm/s,它们同时出发,设运动的时间为t s.
(1)运动几秒时,△APC是等腰三角形?
(2)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
参考答案:
【答案】(1)运动![]() s时,△APC是等腰三角形.(2)当运动时间为5.5 s 或6 s 或6.6 s时,△BCQ为等腰三角形.
s时,△APC是等腰三角形.(2)当运动时间为5.5 s 或6 s 或6.6 s时,△BCQ为等腰三角形.
【解析】
(1)根据题意得,AP=PC,列方程,求解即可;
(2)分BQ=BC,CQ=BC和BQ=CQ三种情况分别讨论得到关于t的方程,求出t即可.
(1)由题意可知AP=t,PC=![]()
∵AP=PC,
∴t=![]() ,
,
解得,t=![]() ,
,
∴出发![]() 秒后△APC能形成等腰三角形;
秒后△APC能形成等腰三角形;
(2)在△ABC中,由勾股定理可求得AC=10,
当点Q在AC上时,AQ=BC+AC-2t=16-2t,所以CQ=AC-AQ=10-(16-2t)=2t-6,
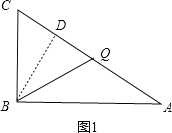
当BQ=BC=6时,如图1,过B作BD⊥AC,则CD=![]() CQ=t-3,在Rt△ABC中,可求得BD=
CQ=t-3,在Rt△ABC中,可求得BD=![]() ,
,
在Rt△BCD中,由勾股定理可得BC2=BD2+CD2,即62=(![]() )2+(t-3)2,
)2+(t-3)2,
解得t=![]() 或t=-
或t=-![]() <0(舍去);
<0(舍去);
当CQ=BC=6时,则2t-6=6,解得t=6,
当CQ=BQ时,则∠C=∠QBC,
∴∠C+∠A=∠CBQ+∠QBA,
∴∠A=∠QBA,
∴QB=QA,
∴CQ=![]() AC=5,即2t-6=5,解得t=5.5,
AC=5,即2t-6=5,解得t=5.5,
综上可知当△BCQ为等腰三角形时,t=![]() 或t=6或t=5.5.
或t=6或t=5.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公园的门票价格是:成人20元/张,学生10元/张,满40人可购买团体票(票价均打八折).设一个共有x人的旅游团去该公园游玩,其中学生有y人.
(1)用含x,y的式子表示该旅游团应付的门票费;
(2)如果旅游团有47人,其中学生有12人,那么他们应付多少元门票费?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从超市出发,向东走了1千米,到达小明家,继续向东走了3千米到达小兵家,然后西走了10千米,到达小华家,最后又向东走了6千米结束行程.
(1)如果以超市为原点,以向东为正方向,用1个单位长度表示1千米,请你在下面的数轴上表示出小明家、小兵家和小华家的具体位置.

(2)请你通过计算说明货车最后回到什么地方?
(3)如果货车行驶1千米的用油量为0.25升,请你计算货车从出发到结束行程共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D、E两点分别在AC、BC上,DE为BC的中垂线,BD为∠ADE的角平分线.若∠A=58°,则∠ABD的度数为何?( )

A.58
B.59
C.61
D.62 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c在数轴上对应点的位置如图所示,

(1)在数轴上标出a,b,c相反数的对应点的位置;
(2)判断下列各式与0的大小:①b+c 0;②a-b 0;③bc 0;④
 0.
0.(3)化简式子:| a | - | a+b | + | c-b | + | a+c | .
-
科目: 来源: 题型:
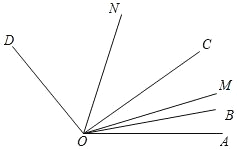
查看答案和解析>>【题目】如图,已知∠AOD=150°,OB、OC、OM、ON 是∠AOD 内的射线,若∠BOC=20°,∠AOB=10°,OM 平分∠AOC,ON 平分∠BOD,当∠BOC 在∠AOD 内绕着点 O以 3°/秒的速度逆时针旋转 t 秒时,当∠AOM:∠DON=3:4 时,则 t=____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆O通过五边形OABCD的四个顶点.若
 =150°,∠A=65°,∠D=60°,则
=150°,∠A=65°,∠D=60°,则 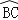 的度数为何?( )
的度数为何?( ) 
A.25
B.40
C.50
D.55
相关试题

