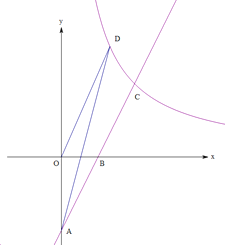
【题目】如图,在平面直角坐标系中,直线![]() 与坐标轴交于
与坐标轴交于![]() 、
、![]() 两点,与反比例函数
两点,与反比例函数![]() 在第一象限内的图像交于点
在第一象限内的图像交于点![]() ,反比例函数图像上有一点
,反比例函数图像上有一点![]() ,连接
,连接![]() 和
和![]() ,已知:
,已知: ![]() .
.
(1)求一次函数和反比例函数的解析式.
(2)求△AOD的面积.
参考答案:
【答案】(1)一次函数解析式为![]() ,反比例函数的解析式为
,反比例函数的解析式为![]() ;
;
(2)△AOD的面积为![]() .
.
【解析】试题分析:(1)先求出A的坐标,根据正切值求出B的坐标,把点B坐标代入一次函数解析式中即可求得k值,从而得到其解析式,把C点横坐标代入,求得纵坐标a的值,再把C点坐标代入![]() 中,可得k值,即可得反比例函数的解析式;(2)把D点纵坐标y=6代入,解得x的值,利用三角形的面积公式可计算.
中,可得k值,即可得反比例函数的解析式;(2)把D点纵坐标y=6代入,解得x的值,利用三角形的面积公式可计算.
试题解析:(1)在![]() 中,当x=0时
中,当x=0时![]() ∴A(0,-4)
∴A(0,-4)
在RtABO中: ![]()
∴OB=2 ∴B(2,0)
将B(2,0)代入![]() 中:k=2
中:k=2
∴![]()
当x=4时,y=4 ∴C(4,4)
∴m=4×4=16
∴![]()
(2)当y=6时,x=![]()
∴D(![]() ,6)
,6)
∴S=![]() =
=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,任意一个正整数
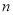 都可以进行这样的分解:
都可以进行这样的分解: 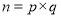 (
(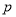 ,
, 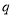 是正整数,且
是正整数,且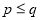 ),在
),在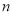 的所有这种分解中,如果
的所有这种分解中,如果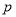 ,
, 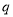 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称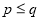 是
是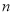 的最佳分解,并规定:
的最佳分解,并规定: 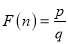 .
.例如
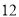 可以分解成
可以分解成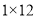 ,
, 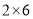 或
或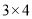 ,因为
,因为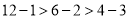 ,所以
,所以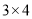 是
是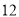 的最佳分解,所以
的最佳分解,所以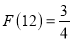 .
.(
 )求出
)求出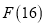 的值.
的值.(
 )如果一个两位正整数
)如果一个两位正整数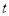 ,
, 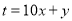 (
(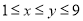 ,
, 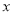 ,
, 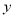 为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为
为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为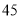 ,那么我们称这个数
,那么我们称这个数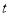 为“文澜数”,求所有“文澜数”并写出所有“文澜数”中
为“文澜数”,求所有“文澜数”并写出所有“文澜数”中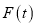 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.张刚按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)张刚在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设张刚获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果张刚想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
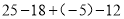
(2)
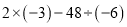
(3)

(4)﹣14﹣2×[5﹣(﹣3)2].
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )

A. b2>4ac
B. ax2+bx+c≥﹣6
C. 若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D. 关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】无论m取什么实数,点A(m+1,2m﹣2)都在直线l上.若点B(a,b)是直线l上的动点,则(2a﹣b﹣6)3的值等于____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,1)与点A′(5,b)关于坐标原点对称,则实数a、b的值是( )
A.a=5,b=1
B.a=﹣5,b=1
C.a=5,b=﹣1
D.a=﹣5,b=﹣1
相关试题

