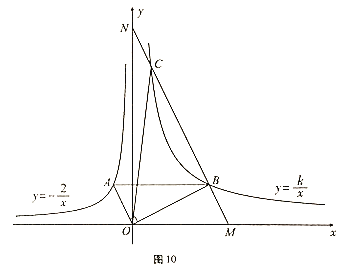
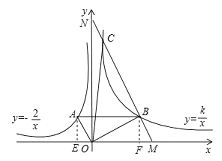
【题目】如图10,![]() ,反比例函数
,反比例函数![]()
![]() 的图象过点
的图象过点![]() ,反比例函数
,反比例函数![]() 的图象过点
的图象过点![]() ,且
,且![]() 轴.
轴.
(1)求![]() 和
和![]() 的值;
的值;
(2)过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,交双曲线
,交双曲线![]() 于另一点,求
于另一点,求![]() 的面积.
的面积.
参考答案:
【答案】(1)a=2,b=8;(2)15.
【解析】试题分析:(1)把A(﹣1,a)代入反比例函数![]() 得到A(﹣1,2),过A作AE⊥x轴于E,BF⊥⊥x轴于F,根据相似三角形的性质得到B(4,2),于是得到k=4×2=8;(2)求的直线AO的解析式为y=﹣2x,设直线MN的解析式为y=﹣2x+b,得到直线MN的解析式为y=﹣2x+10,解方程组得到C(1,8),于是得到结论.
得到A(﹣1,2),过A作AE⊥x轴于E,BF⊥⊥x轴于F,根据相似三角形的性质得到B(4,2),于是得到k=4×2=8;(2)求的直线AO的解析式为y=﹣2x,设直线MN的解析式为y=﹣2x+b,得到直线MN的解析式为y=﹣2x+10,解方程组得到C(1,8),于是得到结论.
试题解析:
(1)∵反比例函数![]() (x<0)的图象过点A(﹣1,a),
(x<0)的图象过点A(﹣1,a),
∴a=﹣![]() =2,
=2,
∴A(﹣1,2),
过A作AE⊥x轴于E,BF⊥⊥x轴于F,
∴AE=2,OE=1,
∵AB∥x轴,
∴BF=2,
∵∠AOB=90°,
∴∠EAO+∠AOE=∠AOE+∠BOF=90°,
∴∠EAO=∠BOF,
∴△AEO∽△OFB,
∴![]() ,
,
∴OF=4,
∴B(4,2),
∴k=4×2=8;
(2)∵直线OA过A(﹣1,2),
∴直线AO的解析式为y=﹣2x,
∵MN∥OA,
∴设直线MN的解析式为y=﹣2x+b,
∴2=﹣2×4+b,
∴b=10,
∴直线MN的解析式为y=﹣2x+10,
∵直线MN交x轴于点M,交y轴于点N,
∴M(5,0),N(0,10),
解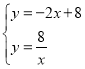 得,
得,![]() 或
或![]() ,
,
∴C(1,8),
∴△OBC的面积=S△OMN﹣S△OCN﹣S△OBM=![]() ×5×10﹣
×5×10﹣![]() ×10×1﹣
×10×1﹣![]() ×5×2=15.
×5×2=15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正数的两个平方根分别是a+3和2﹣2a,则这个正数的立方根是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,其中是中心对称图形有_____个.
①圆;②平行四边形;③长方形;④等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若am=5,an=3,则am+n=_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A.对角线互相平分的四边形是平行四边形
B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直的四边形是正方形 -
科目: 来源: 题型:
查看答案和解析>>【题目】在今年“全国助残日”捐款活动中,某班级第一小组7名同学积极捐出自己的零花钱,奉献自己的爱心,他们捐款的数额分别是(单位:元)50、20、50、30、25、50、55,这组数据的众数和中位数分别是( )
A.50元,30元
B.50元,40元
C.50元,50元
D.55元,50元 -
科目: 来源: 题型:
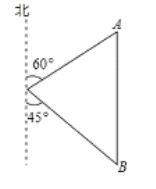
查看答案和解析>>【题目】如图9,小明家在学校
 的北偏东
的北偏东 方向,距离学校80米的
方向,距离学校80米的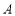 处,小华家在学校
处,小华家在学校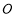 的南偏东
的南偏东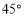 方向的
方向的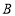 处,小华家在小明家的正南方向,求小华家到学校的距离.(结果精确到1米,参考数据:
处,小华家在小明家的正南方向,求小华家到学校的距离.(结果精确到1米,参考数据: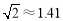 ,
, ,
,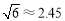 )
)
相关试题

