【题目】如图，四边形ABCD是⊙O的内接四边形，∠ABC=2∠D，连接OA、OB、OC、AC，OB与AC相交于点E．

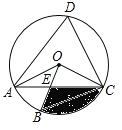
（1）求∠OCA的度数；

（2）若∠COB=3∠AOB，OC=，求图中阴影部分面积（结果保留π和根号）．

参考答案：

【答案】（1）30°；（2）．

【解析】

试题分析：（1）圆内接四边形性质得到∠ABC+∠D=180°，根据∠ABC=2∠D得到∠D+2∠D=180°，从而求得∠D=60°，由OA=OC得到∠OAC=∠OCA=30°；

（2）由∠COB=3∠AOB得到∠AOB=30°，从而有∠COB为直角，然后利用S阴影=S扇形OBC﹣S△OEC求解．

试题解析：（1）∵四边形ABCD是⊙O的内接四边形，∴∠ABC+∠D=180°，∵∠ABC=2∠D，∴∠D+2∠D=180°，∴∠D=60°，∴∠AOC=2∠D=120°，∵OA=OC，∴∠OAC=∠OCA=30°；

（2）∵∠COB=3∠AOB，∴∠AOC=∠AOB+3∠AOB=120°，∴∠AOB=30°，∴∠COB=∠AOC﹣∠AOB=90°，在Rt△OCE中，OC=，∴OE=OCtan∠OCE=tan30°==2，

∴S△OEC=OEOC==，∴S扇形OBC==3π，∴S阴影=S扇形OBC﹣S△OEC=．

关闭