【题目】如图,点E、F分别为菱形ABCD边AD、CD的中点.
(1)求证:BE=BF;
(2)当△BEF为等边三角形时,求证:∠D=2∠A.

参考答案:
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)根据菱形的性质得到AB=CB,AD=CD,∠A=∠C,再根据中点的定义得到AE=CF,根据SAS可证△BAE≌△BCF,根据全等三角形的性质得到BE=BF即可;
(2)作辅助线,先根据线段垂直平分线的逆定理证明BD是EF的垂直平分线,由等边三角形三线合一得:EG=FG,∠EBG=![]() ∠EBF=30°,设EG=x,则BE=2x,BG=
∠EBF=30°,设EG=x,则BE=2x,BG=![]() x,根据中位线定理得:AO=2EG=2x,OB=
x,根据中位线定理得:AO=2EG=2x,OB=![]() x,证明△BHO∽△BEG,列比例式可得OH=
x,证明△BHO∽△BEG,列比例式可得OH= ![]() ,BH=
,BH=![]() x,再求AH=
x,再求AH=![]() x,则AH=BH,可得∠DAB=60°,∠ADC=120°,从而得出结论.
x,则AH=BH,可得∠DAB=60°,∠ADC=120°,从而得出结论.
试题解析:证明:(1)∵四边形ABCD是菱形,∴∠A=∠C,AB=BC=AD=CD.∵点E、F分别为菱形ABCD边AD、CD的中点,∴AE=![]() AD,CF=
AD,CF=![]() CD,∴AE=CF,∴△ABE≌△CBF(SAS),∴BE=BF;
CD,∴AE=CF,∴△ABE≌△CBF(SAS),∴BE=BF;
(2)如图,连接AC、BD交于点O,设BD与EF交于G,AC与BE交于H,则AC⊥BD.∵BE=BF,ED=DF,∴BD是EF的垂直平分线,∴EG=FG,∠EBG=![]() ∠EBF=30°,Rt△BEG中,设EG=x,则BE=2x,BG=
∠EBF=30°,Rt△BEG中,设EG=x,则BE=2x,BG=![]() x.∵EG∥AO,E为AD的中点,∴G是OD的中点,∴AO=2EG=2x,OB=
x.∵EG∥AO,E为AD的中点,∴G是OD的中点,∴AO=2EG=2x,OB=![]() x.∵OH∥GE,∴△BHO∽△BEG,∴
x.∵OH∥GE,∴△BHO∽△BEG,∴![]() ,∴
,∴![]() =
=![]() =
=![]() ,∴OH=
,∴OH= ![]() ,BH=
,BH=![]() x,∴AH=AO﹣OH=2x﹣
x,∴AH=AO﹣OH=2x﹣![]() x=
x=![]() x,∴AH=BH,∴∠HAB=∠ABH.∵∠BHC=∠HAB+∠ABH=60°,∴∠HAB=30°,∴∠DAB=60°,∴∠ADC=120°,∴∠ADC=2∠DAB,即∠D=2∠A.
x,∴AH=BH,∴∠HAB=∠ABH.∵∠BHC=∠HAB+∠ABH=60°,∴∠HAB=30°,∴∠DAB=60°,∴∠ADC=120°,∴∠ADC=2∠DAB,即∠D=2∠A.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定:
(a,b)★(c,d)=bc-ad.
例如:(1,2)★(3,4)=2×3-1×4=2.
根据上述规定解决下列问题:
(1)有理数对(2,-3)★(3,-2)=_______;
(2)若有理数对(-3,2x-1)★(1,x+1)=7,则x=_______;
(3)当满足等式(-3,2x-1)★(k,x+k)=5+2k的x是整数时,求整数k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空: a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
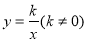 ,在每个象限内y随着x的增大而增大,点P(a-1, 2)在这个反比例函数上,a的值可以是()
,在每个象限内y随着x的增大而增大,点P(a-1, 2)在这个反比例函数上,a的值可以是()A. 0B. 1C. 2D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】按要求画图
(1)如图,平面上有五个点A,B,C,D,E. 按下列要求画出图形.
①连接BD;
②画直线AC交BD于点M;
③过点A作线段AP⊥BD于点P;
④请在直线AC上确定一点N,使B,E两点到点N的距离之和最小(保留作图痕迹).
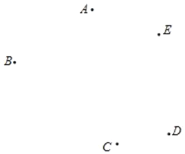
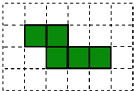
(2)小强用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.注意:只需添加一个符合要求的正方形,并用阴影表示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一些相同的房间需要粉刷墙面.一天3名一级技工去粉刷8个房间,结果其中有50m2墙面未来得及粉刷;同样时间内5名二级技工粉刷了10个房间之外,还多粉刷了另外的40m2墙面.每名一级技工比二级技工一天多粉刷12m2墙面,求一个一级技工和一个二级技工每天粉刷的墙面各是多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
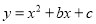 经过点A(1,0)和B(0,3),其顶点为D.
经过点A(1,0)和B(0,3),其顶点为D.(1)求此抛物线的表达式;
(2)求△ABD的面积;
(3)设P为该抛物线上一点,且位于抛物线对称轴右侧,作PH⊥对称轴,垂足为H,若△DPH与△AOB相似,求点P的坐标.
相关试题

