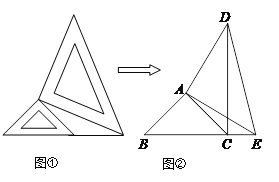
【题目】两个大小不同的等腰直角三角板如图①所示放置,图②是由它抽象出来的几何图形,点B、C、E在同一条直线上,连结DC.
(1)请找出图②中的全等三角形,并给予证明;
(2)求证:DC⊥BE.
参考答案:
【答案】(1)△ACD≌△ABE(2)证明见解析
【解析】试题分析:(1)根据等腰直角三角形的性质可以得出AB=AC,AE=AD,∠BAC=∠EAD,进而得到∠BAE=∠CAD,即可得到结论;
(2)由△ABE≌△ACD可以得出∠ACD=∠ABE,进而得出∠BCD =90°,由此可以得出结论.
试题解析:(1)解:△ACD≌△ABE. 证明如下:
∵△ABC与△AED均为等腰直角三角形,∴AB=AC,AE=AD,∠BAC=∠EAD=90°,∴∠BAC+∠CAE=∠EAD+∠CAE,即∠BAE=∠CAD.
在△ABE与△ACD中,∵AB=AC,∠BAE=∠CAD,AE=AD,∴△ABE≌△ACD(SAS).
(2)证明:∵△ABC是等腰直角三角形,∴∠ABC=∠ACB=45°.
由(1)可知△ABE≌△ACD,∴∠ACD=∠ABE=45°,∴∠BCD=∠ACB+∠ACD=90°,∴DC⊥BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在汕头市“创文”活动中,一项绿化工程由甲、乙两工程队承担.已知甲工程队单独完成这项工作需120天,甲工程队单独工作30天后,乙工程队参与合做,两队又共同工作了36天完成.
(1)求乙工程队单独完成这项工作需要多少天?
(2)因工期的需要,将此项工程分成两部分,甲做其中一部分用了
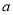 天完成,乙做另一部分用了
天完成,乙做另一部分用了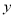 天完成.若乙工程队还有其它工作任务,最多只能做52天.求甲工程队至少应做多少天?
天完成.若乙工程队还有其它工作任务,最多只能做52天.求甲工程队至少应做多少天? -
科目: 来源: 题型:
查看答案和解析>>【题目】如右图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的△ABC,
(2)再在图中画出△ABC的高CD,
(3)在右图中能使S△ABC=S△PBC的格点P的个数有 个(点P异于A)

-
科目: 来源: 题型:
查看答案和解析>>【题目】请写出一个关于x的不等式,使-1,2都是它的解__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠ABC=∠ACB,D为线段CB上一点(不与C、B重合),点E为射线CA上一点,∠ADE=∠AED.设∠BAD=α,∠CDE=β.
(1)如图(1),
①若∠BAC=42°,∠DAE=30°,则α= ,β= .
②若∠BAC=54°,∠DAE=36°,则α= ,β= .
③写出α与β的数量关系,并说明理由;

(2)如图(2),当E点在CA的延长线上时,其它条件不变,请直接写出α与β的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2.
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(a2)3·(a2-2ab+1).
相关试题

