【题目】若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是( )
A.矩形 B.菱形
C.对角线互相垂直的四边形 D.对角线相等的四边形
参考答案:
【答案】C
【解析】
试题分析:此题要根据矩形的性质和三角形中位线定理求解;首先根据三角形中位线定理知:所得四边形的对边都平行且相等,那么其必为平行四边形,若所得四边形是矩形,那么邻边互相垂直,故原四边形的对角线必互相垂直,由此得解.
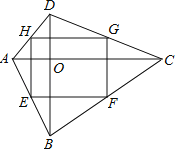
解:已知:如右图,四边形EFGH是矩形,且E、F、G、H分别是AB、BC、CD、AD的中点,求证:四边形ABCD是对角线垂直的四边形.
证明:由于E、F、G、H分别是AB、BC、CD、AD的中点,
根据三角形中位线定理得:EH∥FG∥BD,EF∥AC∥HG;
∵四边形EFGH是矩形,即EF⊥FG,
∴AC⊥BD,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=
 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=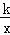 的图象上,则k的值为( )
的图象上,则k的值为( )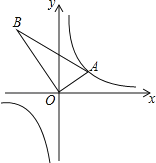
A.﹣4 B.4 C.﹣2 D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示0.000034,结果是 ( )
A. 3.4×10-5 B. 3.4×10-4 C. 0.34×10-4 D. 34×10-6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.

(1)求∠2、∠3的度数;
(2)求长方形纸片ABCD的面积S.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个多边形的内角总和是900°,且边数之比是1∶2,求这两个多边形的边数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,∠A,∠B,∠C,∠D的度数之比为2∶3∶4∶3,则∠D等于( )
A. 60° B. 75° C. 90° D. 120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若双曲线y=
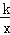 与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=2BD.则实数k的值为 .
与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=2BD.则实数k的值为 .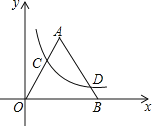
相关试题

