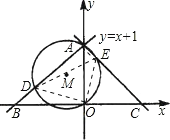
【题目】(12分)如图末-10,在平面直角坐标系中,直线y=x+1与y轴交于点A,与x轴交于点B,点C和点B关于y轴对称.
(1)求△ABC内切圆的半径;
(2)过O、A两点作⊙M,分别交直线AB、AC于点D、E,求证:AD+AE是定值,并求其值.

参考答案:
【答案】(1)![]() -1;(2)
-1;(2)![]()
【解析】试题分析:(1)因为直线y=x+1与y轴交于点A,与x轴交于点B,点C和点B关于y轴对称,所以分别令![]() 即可求出点
即可求出点![]() 的坐标,由此即可求出OA=OB=OC=1,所以可判断
的坐标,由此即可求出OA=OB=OC=1,所以可判断![]() 为Rt△,
为Rt△, ![]() 所以
所以![]() 代入相关数据即可求出内切圆的半径
代入相关数据即可求出内切圆的半径![]() ;
;
(2)连接OD,OE,DE.AE,因为![]() 根据
根据![]() 的圆周角对的弦是直径可得DE为直径,所以
的圆周角对的弦是直径可得DE为直径,所以![]() 又因
又因![]() 利用同角的余角相等可得
利用同角的余角相等可得![]() 因为
因为![]() 且OA=OB.可得△AOE≌△BOD.故AE=BD.所以
且OA=OB.可得△AOE≌△BOD.故AE=BD.所以![]()
试题解析:(1)∵直线AB的解解析式为:y=x+1,
∴A(0,1),B(1,0),
∵点C和点B关于y轴对称,
∴点C(1,0),
∴OA=OB=OC=1,
∵△ABC为Rt△, ![]()
∴![]() ,即内切圆的半径为
,即内切圆的半径为![]()
(2)连接OD,OE,DE.AE,
∵![]()
∴DE为直径.∴![]()
又∵![]()
又∵![]() 且OA=OB.
且OA=OB.
∴△AOE≌△BOD.故AE=BD.
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
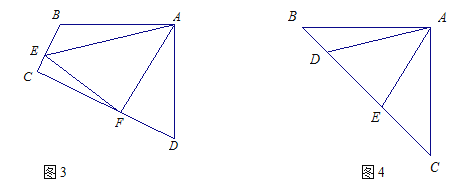
小炎遇到这样一个问题:如图1,点E、F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连结EF,则EF=BE+DF,试说明理由.

小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.她先后尝试了翻折、旋转、平移的方法,最后发现线段AB,AD是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG,再利用全等的知识解决了这个问题(如图2).
参考小炎同学思考问题的方法,解决下列问题:
(1)如图3,四边形ABCD中,AB=AD,∠BAD=90°点E,F分别在边BC,CD上,∠EAF=45°.若∠B,∠D都不是直角,则当∠B与∠D满足_ 关系时,仍有EF=BE+DF;
(2)如图4,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,若BD=1, EC=2,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期
一
二
三
四
五
六
日
增减
-5
+7
-3
+4
+10
-9
-25
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)

(2)
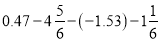
(3)
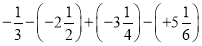
(4)
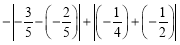
(5)
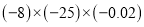
(6)
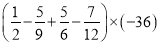
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某中学七年级5名学生的体重情况:
姓名
小颖
小明
小刚
小京
小宁
体重(千克)
34
45
体重与平均体重的差
-6
+3
-4
0
(1)完成上表.
(2)谁最重?谁最轻?
(3)最重的与最轻的相差多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了开展“阳光体育运动”,计划购买篮球与足球共
 个,已知每个篮球的价格为
个,已知每个篮球的价格为 元,每个足球的价格为
元,每个足球的价格为 元
元(1)若购买这两类球的总金额为
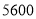 元,求篮球和足球各购买了多少个?
元,求篮球和足球各购买了多少个?(2)元旦期间,商家给出蓝球打九折,足球打八五折的优惠价,若购买这种篮球与足球各
 个,那么购买这两类球一共需要多少钱?
个,那么购买这两类球一共需要多少钱? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0,其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
相关试题

