搜索
【题目】如图，在平行四边形ABCD中，P是CD边上一点，且AP和BP分别平分∠DAB和∠CBA，若AD=5，AP=8，则△APB的周长是 ．
参考答案：
【答案】24.
【解析】
试题分析： ∵四边形ABCD是平行四边形，∴AD∥CB，AB∥CD，∴∠DAB+∠CBA=180°，又∵AP和BP分别平分∠DAB和∠CBA，∴∠PAB=
∠DAB，∠PBA=∠ABC，∴∠PAB+∠PBA=（∠DAB+∠CBA）=90°，∴∠APB=180°﹣（∠PAB+∠PBA）=90°；∵AB∥CD，∴∠PAB=∠DPA，∴∠DAP=∠DPA，∴AD=DP=5，同理：PC=CB=5，
即AB=DC=DP+PC=10，在Rt△APB中，AB=10，AP=8，∴BP=
=6，∴△APB的周长=6+8+10=24.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，点A的坐标为(1，1)，点B的坐标为(11，1)，点C到直线AB的距离为4，三角形ABC是直角三角形且∠C不是直角，则满足条件的点C有________个．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）【证法回顾】证明：三角形中位线定理．
已知：如图1，DE是△ABC的中位线．
求证： ．
证明：添加辅助线：如图1，在△ABC中，延长DE （D、E分别是AB、AC的中点）到点F，使得EF=DE，连接CF；
请继续完成证明过程：
（2）【问题解决】
如图2，在正方形ABCD中，E为AD的中点，G、F分别为AB、CD边上的点，若AG=2，DF=3，∠GEF=90°，求GF的长．
（3）【拓展研究】
如图3，在四边形ABCD中，∠A=105°，∠D=120°，E为AD的中点，G、F分别为AB、CD边上的点，若AG=
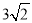，DF=2，∠GEF=90°，求GF的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】我们把分子为1的分数叫做单位分数，如
， 
， 
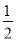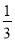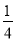，…任何一个单位分数都可以拆分成两个不同的单位分数的和，如
=
+
， 
=
+
， 
=
+
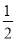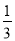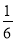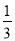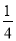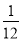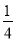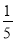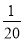，…（1）根据对上述式子的观察，你会发现
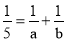则a= ，b= ；进一步思考，单位分数
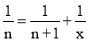(n是不小于2的正整数）则x= （用n的代数式表示）计算：
-
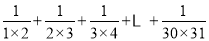
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行四边形ABCD中，过点B作BE∥AC，在BG上取点E，连接DE交AC的延长线于点F．
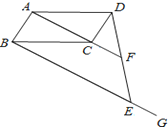
（1）求证：DF=EF；
（2）如果AD=6，∠ADC=60°，AC⊥DC于点C，AC=2CF，求BE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“x的2倍与3的差不大于8”列出的不等式是（ ）
A. 2x-3≤8 B. 2x-3≥8 C. 2x-3<8 D. 2x-3>8
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列方程有两个相等的实数根的是( )
A. x2＋x＋1＝0 B. 4x2＋2x＋1＝0 C. x2＋12x＋36＝0 D. x2＋x－2＝0
相关试题
