【题目】(1)【证法回顾】证明:三角形中位线定理.
已知:如图1,DE是△ABC的中位线.
求证: .
证明:添加辅助线:如图1,在△ABC中,延长DE (D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;
请继续完成证明过程:

(2)【问题解决】
如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)【拓展研究】
如图3,在四边形ABCD中,∠A=105°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=![]() ,DF=2,∠GEF=90°,求GF的长.
,DF=2,∠GEF=90°,求GF的长.
参考答案:
【答案】(1)DE∥BC,DE=![]() BC,证明见解析;(2)5; (3)
BC,证明见解析;(2)5; (3) ![]() .
.
【解析】(1)分析:根据三角形的中位线定理填写即可;利用“边角边”证明△ADE和△CFE全等,根据全等三角形对应角相等可得∠A=∠ECF,全等三角形对应边相等可得AD=CF,然后求出四边形BCFD是平行四边形,根据平行四边形的性质证明即可.(2)由,正方形性质及E为AD 中点得出△ADE≌△CFE,由全等三角形推出,EF垂直平分GH,从而求解.(3) 过点D作AB的平行线交GE的延长线于点H,过H作CD的垂线,垂足为P,连接HF,可证明△AEG≌△DEH,结合条件可得到△HPD为等腰直角三角形,可求得PF的长,在Rt△HFP中,可求得HF,则可求得GF的长.
(1)DE∥BC,DE=![]() BC
BC
证明:在△ADE和△CFE中, 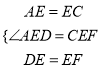 ,∴△ADE≌△CFE(SAS),
,∴△ADE≌△CFE(SAS),
∴∠A=∠ECF,AD=CF,∴CF∥AB,又∵AD=BD,∴CF=BD,
∴四边形BCFD是平行四边形,∴DE∥BC,DE=![]() BC.
BC.
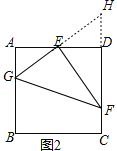
(2)如图2,延长GE、FD交于点H,
∵E为AD中点,
∴EA=ED,且∠A=∠EDH=90°,
在△AEG和△DEH中
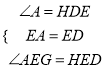 ∴△AEG≌△DEH(ASA),
∴△AEG≌△DEH(ASA),
∴AG=HD=2,EG=EH,∵∠GEF=90°,∴EF垂直平分GH,
∴GF=HF=DH+DF=2+3=5;
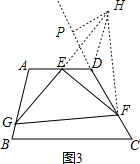
(3)如图3,过点D作AB的平行线交GE的延长线于点H,过H作CD的垂线,垂足为P,连接HF,
同(1)可知△AEG≌△DEH,GF=HF,∴∠A=∠HDE=105°,AG=HD=![]() ,
,
∵∠ADC=120°,∴∠HDF=360°﹣105°﹣120°=135°,
∴∠HDP=45°,∴△PDH为等腰直角三角形,
∴PD=PH=3,∴PF=PD+DF=3+2=5,
在Rt△HFP中,∠HPF=90°,HP=3,PF=5,
∴HF=![]() ==
==![]() ∴GF=
∴GF=![]() .
.
点睛;本题考查了四边形的综合应用,考查了正方形的性质,全等三角形的判定和性质,等腰三角形的性质,勾股定理;本题考查知识点较多综合性较强,难度较大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一条两岸平行的河流,一数学实践活动小组在无法涉水过河情况下,成功测得河的宽度,他们的做法如下:
①正对河流对岸的一颗树A,在河的一岸选定一点B;
②沿河岸直走15步恰好到达一树C处,继续前行15步到达D处;
③自D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处时,停止行走;
④测得DE的长就是河宽.
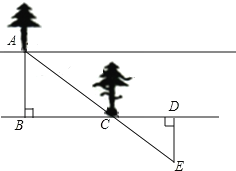
请你运用所学知识说明他们做法是正确的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】六边形的外角和是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标为(1,1),点B的坐标为(11,1),点C到直线AB的距离为4,三角形ABC是直角三角形且∠C不是直角,则满足条件的点C有________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把分子为1的分数叫做单位分数,如
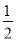 ,
, 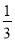 ,
, 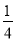 ,…任何一个单位分数都可以拆分成两个不同的单位分数的和,如
,…任何一个单位分数都可以拆分成两个不同的单位分数的和,如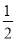 =
=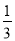 +
+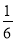 ,
, 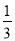 =
=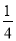 +
+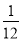 ,
, 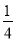 =
=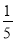 +
+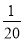 ,…
,…(1)根据对上述式子的观察,你会发现
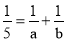 则a= ,b= ;
则a= ,b= ;进一步思考,单位分数
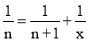 (n是不小于2的正整数)则x= (用n的代数式表示)
(n是不小于2的正整数)则x= (用n的代数式表示)计算:
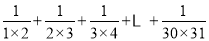
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过点B作BE∥AC,在BG上取点E,连接DE交AC的延长线于点F.
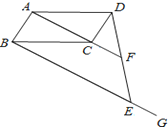
(1)求证:DF=EF;
(2)如果AD=6,∠ADC=60°,AC⊥DC于点C,AC=2CF,求BE的长.
相关试题

