搜索
【题目】我们把分子为1的分数叫做单位分数，如
， 
， 
，…任何一个单位分数都可以拆分成两个不同的单位分数的和，如
=
+
， 
=
+
， 
=
+
，…
（1）根据对上述式子的观察，你会发现
则a= ，b= ；
进一步思考，单位分数
(n是不小于2的正整数）则x= （用n的代数式表示）
计算： 
参考答案：
【答案】（1）a=6,b=30; (2)x=n(n+1) (3) 
【解析】根据题中所给规律可以发现，一个单位分数等于比这个单位分数的分母大的数的单位分数和这个单位分数的分母的数与比这个单位分数的分母大的数的积的单位分数的和，即
（n是不小于的正整数）,由规律即可求解.
本题解析：
（1）由题意得： 
，∴a=6, b=30；
∴
，∵
，∴x=n(n+1)
计算：原式=
-
科目： 来源： 题型：
查看答案和解析>>【题目】六边形的外角和是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，点A的坐标为(1，1)，点B的坐标为(11，1)，点C到直线AB的距离为4，三角形ABC是直角三角形且∠C不是直角，则满足条件的点C有________个．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）【证法回顾】证明：三角形中位线定理．
已知：如图1，DE是△ABC的中位线．
求证： ．
证明：添加辅助线：如图1，在△ABC中，延长DE （D、E分别是AB、AC的中点）到点F，使得EF=DE，连接CF；
请继续完成证明过程：
（2）【问题解决】
如图2，在正方形ABCD中，E为AD的中点，G、F分别为AB、CD边上的点，若AG=2，DF=3，∠GEF=90°，求GF的长．
（3）【拓展研究】
如图3，在四边形ABCD中，∠A=105°，∠D=120°，E为AD的中点，G、F分别为AB、CD边上的点，若AG=
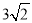，DF=2，∠GEF=90°，求GF的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行四边形ABCD中，P是CD边上一点，且AP和BP分别平分∠DAB和∠CBA，若AD=5，AP=8，则△APB的周长是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行四边形ABCD中，过点B作BE∥AC，在BG上取点E，连接DE交AC的延长线于点F．
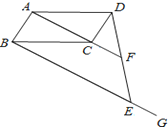
（1）求证：DF=EF；
（2）如果AD=6，∠ADC=60°，AC⊥DC于点C，AC=2CF，求BE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“x的2倍与3的差不大于8”列出的不等式是（ ）
A. 2x-3≤8 B. 2x-3≥8 C. 2x-3<8 D. 2x-3>8
相关试题
