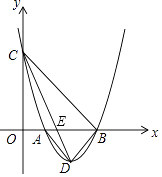
【题目】如图,抛物线y=a(x﹣1)(x﹣3)与x轴交于A,B两点,与y轴的正半轴交于点C,其顶点为D.
(1)写出C,D两点的坐标(用含a的式子表示);
(2)设S△BCD:S△ABD=k,求k的值;
(3)当△BCD是直角三角形时,求对应抛物线的解析式.
参考答案:
【答案】
(1)
解:在y=a(x﹣1)(x﹣3),令x=0可得y=3a,
∴C(0,3a),
∵y=a(x﹣1)(x﹣3)=a(x2﹣4x+3)=a(x﹣2)2﹣a,
∴D(2,﹣a);
(2)
解:在y=a(x﹣1)(x﹣3)中,令y=0可解得x=1或x=3,
∴A(1,0),B(3,0),
∴AB=3﹣1=2,
∴S△ABD= ![]() ×2×a=a,
×2×a=a,
如图,设直线CD交x轴于点E,设直线CD解析式为y=kx+b,
把C、D的坐标代入可得 ![]() ,解得
,解得 ![]() ,
,
∴直线CD解析式为y=﹣2ax+3a,令y=0可解得x= ![]() ,
,
∴E( ![]() ,0),
,0),
∴BE=3﹣ ![]() =
= ![]()
∴S△BCD=S△BEC+S△BED= ![]() ×
× ![]() ×(3a+a)=3a,
×(3a+a)=3a,
∴S△BCD:S△ABD=(3a):a=3,
∴k=3;
(3)
解:∵B(3,0),C(0,3a),D(2,﹣a),
∴BC2=32+(3a)2=9+9a2,CD2=22+(﹣a﹣3a)2=4+16a2,BD2=(3﹣2)2+a2=1+a2,
∵∠BCD<∠BCO<90°,
∴△BCD为直角三角形时,只能有∠CBD=90°或∠CDB=90°两种情况,
①当∠CBD=90°时,则有BC2+BD2=CD2,即9+9a2+1+a2=4+16a2,解得a=﹣1(舍去)或a=1,此时抛物线解析式为y=x2﹣4x+3;
②当∠CDB=90°时,则有CD2+BD2=BC2,即4+16a2+1+a2=9+9a2,解得a=﹣ ![]() (舍去)或a=
(舍去)或a= ![]() ,此时抛物线解析式为y=
,此时抛物线解析式为y= ![]() x2﹣2
x2﹣2 ![]() x+
x+ ![]() ;
;
综上可知当△BCD是直角三角形时,抛物线的解析式为y=x2﹣4x+3或y= ![]() x2﹣2
x2﹣2 ![]() x+
x+ ![]() .
.
【解析】(1)令x=0可求得C点坐标,化为顶点式可求得D点坐标;(2)令y=0可求得A、B的坐标,结合D点坐标可求得△ABD的面积,设直线CD交x轴于点E,由C、D坐标,利用待定系数法可求得直线CD的解析式,则可求得E点坐标,从而可表示出△BCD的面积,可求得k的值;(3)由B、C、D的坐标,可表示出BC2、BD2和CD2 , 分∠CBD=90°和∠CDB=90°两种情况,分别利用勾股定理可得到关于a的方程,可求得a的值,则可求得抛物线的解析式.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
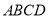 的对角线
的对角线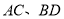 交于点
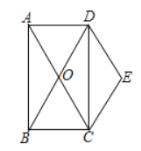
交于点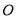 ,且
,且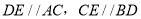 .
.
(1)求证:四边形
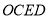 是菱形;
是菱形;(2)若
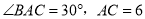 ,求菱形
,求菱形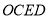 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(﹣2,0),点C(8,0),与y轴交于点A.

(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家研究发现,一般情况下,一节课
 分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为 理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数
分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为 理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数 随时间
随时间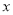 (分钟)的变化规律如图所示(其中
(分钟)的变化规律如图所示(其中 都为线段)
都为线段)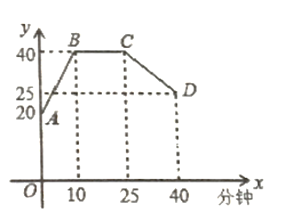
(1)分别求出线段
 和
和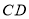 的函数解析式;
的函数解析式;(2)开始上课后第
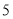 分钟时与第
分钟时与第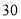 分钟时相比较,何时学生的注意力更集中?
分钟时相比较,何时学生的注意力更集中?(3)一道数学竞赛题,需要讲
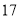 分钟,为了效果较好,要求学生的注意力指标数最低达到
分钟,为了效果较好,要求学生的注意力指标数最低达到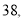 那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目? -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料I:
教材中我们学习了:若关于
 的一元二次方程
的一元二次方程 的两根为
的两根为
 ,根据这一性质,我们可以求出己知方程关于
,根据这一性质,我们可以求出己知方程关于 的代数式的值.
的代数式的值.问题解决:
(1)已知
 为方程
为方程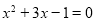 的两根,则:
的两根,则: __ _,
__ _, __ _,那么_
__ _,那么_ (请你完成以上的填空)
(请你完成以上的填空)阅读材料:II
已知
 ,且
,且 .求
.求 的值.
的值.解:由
 可知
可知


又
 且
且 ,即
,即
 是方程
是方程 的两根.
的两根.
问题解决:
(2)若
 且
且 则
则 ;
;(3)已知
 且
且 .求
.求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与 轴交于两点
轴交于两点 和
和 与
与 轴交于点
轴交于点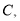 动点
动点 沿
沿 的边
的边 以每秒
以每秒 个单位长度的速度由起点
个单位长度的速度由起点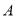 向终点
向终点 运动,过点
运动,过点 作
作 轴的垂线,交
轴的垂线,交 的另一边
的另一边 于点
于点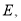 将
将 沿
沿 折叠,使点
折叠,使点 落在点
落在点 处,设点
处,设点 的运动时间为
的运动时间为 秒.
秒.
(1)求抛物线的解析式;
(2)N为抛物线上的点(点
 不与点
不与点 重合)且满足
重合)且满足 直接写出
直接写出 点的坐标;
点的坐标;(3)是否存在某一时刻
 ,使
,使 的面积最大,若存在,求出
的面积最大,若存在,求出 的值和最大面积;若不存在,请说明理由.
的值和最大面积;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】从甲地到乙地有
 三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:公交车用时的频数
公交车用时线路




合计

59
151
166
124
500

50
50
122
278
500

45
265
160
30
500
早高峰期间,乘坐_________(填“
 ”,“
”,“ ”或“
”或“ ”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
相关试题

