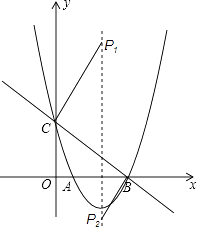
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,与y轴相交于点C,直线y=kx+n(k≠0)经过B,C两点,已知A(1,0),C(0,3),且BC=5.
(1)分别求直线BC和抛物线的解析式(关系式);
(2)在抛物线的对称轴上是否存在点P,使得以B,C,P三点为顶点的三角形是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:∵C(0,3),即OC=3,BC=5,
∴在Rt△BOC中,根据勾股定理得:OB= ![]() =4,即B(4,0),
=4,即B(4,0),
把B与C坐标代入y=kx+n中,得: ![]() ,
,
解得:k=﹣ ![]() ,n=3,
,n=3,
∴直线BC解析式为y=﹣ ![]() x+3;
x+3;
由A(1,0),B(4,0),设抛物线解析式为y=a(x﹣1)(x﹣4)=ax2﹣5ax+4a,
把C(0,3)代入得:a= ![]() ,
,
则抛物线解析式为y= ![]() x2﹣
x2﹣ ![]() x+3
x+3
(2)解:存在.
如图所示,分两种情况考虑:
∵抛物线解析式为y= ![]() x2﹣
x2﹣ ![]() x+3,
x+3,
∴其对称轴x=﹣ ![]() =﹣
=﹣ ![]() =
= ![]() .
.
当P1C⊥CB时,△P1BC为直角三角形,
∵直线BC的斜率为﹣ ![]() ,
,
∴直线P1C斜率为 ![]() ,
,
∴直线P1C解析式为y﹣3= ![]() x,即y=
x,即y= ![]() x+3,
x+3,
与抛物线对称轴方程联立得 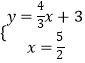 ,
,
解得: 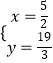 ,
,
此时P( ![]() ,
, ![]() );
);
当P2B⊥BC时,△BCP2为直角三角形,
同理得到直线P2B的斜率为 ![]() ,
,
∴直线P2B方程为y= ![]() (x﹣4)=
(x﹣4)= ![]() x﹣
x﹣ ![]() ,
,
与抛物线对称轴方程联立得: 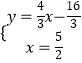 ,
,
解得: 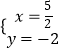 ,
,
此时P2( ![]() ,﹣2).
,﹣2).
综上所示,P1( ![]() ,
, ![]() )或P2(
)或P2( ![]() ,﹣2).
,﹣2).
当点P为直角顶点时,设P( ![]() ,y),
,y),
∵B(4,0),C(0,3),
∴BC=5,
∴BC2=PC2+PB2,即25=( ![]() )2+(y﹣3)2+(
)2+(y﹣3)2+( ![]() ﹣4)2+y2,解得y=
﹣4)2+y2,解得y= ![]() ,
,
∴P3( ![]() ,
, ![]() ),P4(
),P4( ![]() ,
, ![]() ).
).
综上所述,P1( ![]() ,
, ![]() ),P2(
),P2( ![]() ,﹣2),P3(
,﹣2),P3( ![]() ,
, ![]() ),P4(
),P4( ![]() ,
, ![]() ).
).
【解析】(1)利用勾股定理求出B坐标,再把A、C坐标代入解析式即可;(2)“以B,C,P三点为顶点的三角形是直角三角形”须分类讨论:点P为直角顶点;点C为直角顶点;点B为直角顶点;分别过C、B作垂线与对称轴相交,当P为直角顶点时,可利用勾股定理列方程.
-
科目: 来源: 题型:
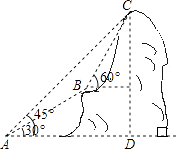
查看答案和解析>>【题目】如图,某电信部门计划修建一条连接B,C两地的电缆.测量人员在山脚A点测得B,C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200m,电缆BC至少长多少米(精确到1m)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于m的方程
 (m-16)=7的解也是关于x的方程2(x-3)-n=52的解.
(m-16)=7的解也是关于x的方程2(x-3)-n=52的解.(1)求m,n的值;
(2)已知∠AOB=m°,在平面内画一条射线OP,恰好使得∠AOP=n∠BOP,求∠BOP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:小明遇到这样一个问题:
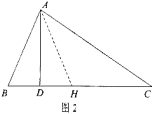
如图1,在△ABC中,∠B=2∠C,AD⊥BC于点D,求证:BC=AB+2BD.
小明利用条件AD⊥BC,在CD上截取DH=BD,如图2,连接AH,既构造了等腰△ABH,又得到BH=2BD,从而命题得证。
(1)根据阅读材料,证明:BC=AB+2BD;
(2)参考小明的方法,解决下面的问题:
如图3,在△ABC中,∠BAC=90°,∠ABD=∠BCE,∠ABC=∠DCE,请探究AD与BE的数量关系,并说明理由。


-
科目: 来源: 题型:
查看答案和解析>>【题目】随着出行方式的多样化,某地区打车有三种乘车方式,收费标准如下(假设打车的平均车速为30千米/小时):
网约出租车
网约顺风车
网约专车
3千米以内:12元
1.5元/千米
2元/千米
超过3千米的部分:2.4元/千米
0.5元/分钟
0.6元/分钟
(如:乘坐6千米,耗时12分钟,网约出租车的收费为:12+2.4×(6-3)=19.2(元);网约顺风车的收费为:6×1.5+12×0.5=15(元);网约专车的收费为:6×2+12×0.6=19.2(元))
请据此信息解决如下问题:
(1)王老师乘车从纵棹园去汽车站,全程8千米,如果王老师乘坐网约出租车,需要支付的打车费用为______元;
(2)李校长乘车从纵掉园去生态园,乘坐网约顺风车比乘坐网约出租车节省了2元.求从纵棹园去生态园的路程;
(3)网约专车为了和网约顺风车竞争客户,分别推出了优惠方式:网约顺风车对于乘车路程在5千米以上(含5千米)的客户每次收费立减6元;网约专车打车车费一律七五折优惠.对采用哪一种打车方式更合算提出你的建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】母亲节前夕,某淘宝店主从厂家购进A、B两种礼盒,已知A、B两种礼盒的单价比为2:3,单价和为200元.
(1)求A、B两种礼盒的单价分别是多少元?
(2)该店主购进这两种礼盒恰好用去9600元,且购进A种礼盒最多36个,B种礼盒的数量不超过A种礼盒数量的2倍,共有几种进货方案?
(3)根据市场行情,销售一个A种礼盒可获利10元,销售一个B种礼盒可获利18元.为奉献爱心,该店主决定每售出一个B种礼盒,为爱心公益基金捐款m元,每个A种礼盒的利润不变,在(2)的条件下,要使礼盒全部售出后所有方案获利相同,m值是多少?此时店主获利多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】有5张边长为2的正方形纸片,4张边长分别为2、3的矩形纸片,6张边长为3的正方形纸片,从其中取出若干张纸片,且每种纸片至少取一张,把取出的这些纸片拼成一个正方形(原纸张进行无空隙、无重叠拼接),则拼成正方形的边长最大为 ( )
A. 6B. 7C. 8D. 9
相关试题

