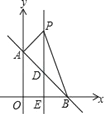
【题目】如图,平面直角坐标系中,直线AB:y=﹣x+b交y轴于点A(0,4),交x轴于点B.
(1)求直线AB的表达式和点B的坐标;
(2)直线l垂直平分OB交AB于点D,交x轴于点E,点P是直线l上一动点,且在点D的上方,设点P的纵坐标为n.
①用含n的代数式表示△ABP的面积;
②当S△ABP=8时,求点P的坐标;
③在②的条件下,以PB为斜边在第一象限作等腰直角△PBC,求点C的坐标.
参考答案:
【答案】(1)AB:y=-x+4,B(4,0);(2)①S△ABP=2n-4,②P(2,6),③C(6,4).
【解析】试题分析:
(1)把点A(0,4)代入y=﹣x+b解得b的值,即可得到一次函数的解析式,由解析式即可求得点B的坐标;
(2)①由(1)中所求点B的坐标为(4,0)结合题意可知,直线PE为: ![]() ,由此可求得点D的坐标,从而可用含“n”的代数式表达出PD的长,由S△ABP=
,由此可求得点D的坐标,从而可用含“n”的代数式表达出PD的长,由S△ABP=![]() PD·OB即可用含“n”表达的面积;
PD·OB即可用含“n”表达的面积;
②将S△ABP=8代入①中所求的表达式中,解方程即可求得“n”的值,从而可得此时点P的坐标;
③如下图,设点C1和C2是符合题意的点C,则由题意易得:四边形BC1PC2是正方形,过点C1作C1M⊥x轴于点M,过点P作PN存在MC1于点N,则四边形PEMN是矩形,△C1MB≌△PNC1;设BM= ![]() ,则C1M=MN-NC1=
,则C1M=MN-NC1= ![]() ;在Rt△PBE中,由勾股定理可求得:PB=
;在Rt△PBE中,由勾股定理可求得:PB=![]() ;再在Rt△BMC1中,由BM2+C1M2=BC12,建立关于“
;再在Rt△BMC1中,由BM2+C1M2=BC12,建立关于“![]() ”分方程,解方程求得“
”分方程,解方程求得“![]() ”的值,即可求得点C1的坐标;同理可求得点C2的坐标;最后结合点C在第一象限这一条件即可得到点C的坐标.
”的值,即可求得点C1的坐标;同理可求得点C2的坐标;最后结合点C在第一象限这一条件即可得到点C的坐标.
试题解析:
(1)∵直线AB:y=﹣x+b交y轴于点A(0,4),
∴b=4,
∴直线AB的表达式为:y=﹣x+4.
∵在y=﹣x+4中,当y=0时,x=4,
∴直线AB与x轴的交点B的坐标为(4,0);
(2)①∵点B的坐标为(4,0),
∴OB=4,
∵直线l垂直平分OB交AB于点D,交x轴于点E,
∴点D的横坐标为2,
∵在y=-x+4中,当x=2时,y=-2+4=2,
∴点D的坐标为(2,2).
∵P是直线l上一动点,且在点D的上方,点P的纵坐标为n,
∴PD=n-2,
∴S△ABP=![]() PD·OB=
PD·OB=![]() ;
;
②当S△ABP=8时,由![]() 解得:
解得: ![]() ,
,
∴此时点P的坐标为(2,6);
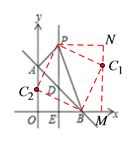
③如图,设点C1和C2是符合题意的点C,则由题意易得:四边形BC1PC2是正方形,过点C1作C1M⊥x轴于点M,过点P作PN存在MC1于点N,则四边形PEMN是矩形,△C1MB≌△PNC1,
∴MN=PE=6,NC1=BM,PN=C1M=BM+BE,
设BM= ![]() ,则C1M=MN-NC1=
,则C1M=MN-NC1= ![]() .
.
∵在Rt△PBE中,PE=6,BE=![]() OB=2,
OB=2,
∴PB=![]() ,
,
又∵PB是等腰Rt△PC1B的斜边,
∴BC1=![]() .
.
∵在Rt△BMC1中,BM2+C1M2=BC12,
∴![]() ,解得:
,解得: ![]() ,
,
∵当![]() 时,PN=C1M=6-4=2<BM+BE,
时,PN=C1M=6-4=2<BM+BE,
∴![]() 只能取2,
只能取2,
∴BM=2,C1M=6-2=4,
∴OM=OB+BM=4+2=6,
∴点C1的坐标为(6,4);
同理可求得点C2的坐标为(0,2);
又∵点C在第一象限,
∴点C的坐标为(6,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中:①线段;②有一个角是30°的直角三角形;③角;④等腰三角形,其中一定是轴对称图形有( )个
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】为促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中的折线反映了每户居民每月用电电费y(单位:元)与用电量x(单位:度)间的函数关系.
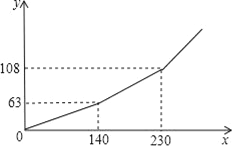
(1)根据图象,阶梯电价方案分为三个档次,请填写下表:

(2)小明家某月用电70度,需交电费 元;
(3)求第二档每月电费y(元)与用电量x(单位:度)之间的函数表达式;
(4)在每月用电量超过230度时,每度电比第二档多m元,小刚家某月用电290度,缴纳电费153元,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B分别是x轴上位于原点左右两侧的两点,点P(2,p)在第一象限内,直线PA交y轴与点C(0,2),直线PB交y轴与点D,且S△AOP=4,
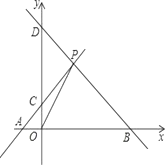
(1)求S△COP;
(2)求点A的坐标及p的值;
(3)若3S△AOP=S△BOP,求直线BD的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)如图1,在四边形ABCD中添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.
(2)问题探究
小红提出了一个猜想:对角线互相平分且相等的“等邻边四边形”是正方形.她的猜想正确吗?请说明理由.
(3)如图2,“等邻边四边形”ABCD中,AB=AD,∠BAD+∠BCD=90°,AC,BD为对角线,AC=
 AB.试探究线段BC,CD,BD之间的数量关系,并证明你的结论.
AB.试探究线段BC,CD,BD之间的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】李克强总理在2017年政府工作报告中指出,今年公路水运投资为1.8万亿元,其中“1.8万亿元”用科学记数法表示为( )
A.1.8×108元
B.1.8×1012元
C.18×1011元
D.0.18×1012元 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 面积相等的两个三角形全等
B. 全等三角形的面积一定相等
C. 形状相同的两个三角形全等
D. 两个等边三角形一定全等
相关试题

