【题目】快、慢两车分别从相距180千米的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早![]() 小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中y(千米)与x(小时)的函数关系式;
(3)两车出发后经过多长时间相距90千米的路程?
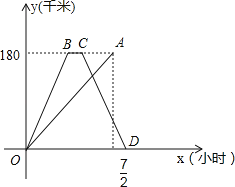
参考答案:
【答案】(1)快车、慢车速度分别为120千米/时,60千米/时;(2)y=﹣120x+420(2≤x≤![]() );(3)两车出发后经过
);(3)两车出发后经过![]() 或
或![]() 或
或![]() 小时相距90千米的路程
小时相距90千米的路程
【解析】试题分析:(1)根据路程与相应的时间,求得慢车的速度,再根据慢车速度是快车速度的一半,求得快车速度;
(2)先求得点C的坐标,再根据点D的坐标,运用待定系数法求得CD的解析式;
(3)分三种情况:在两车相遇之前;在两车相遇之后;在快车返回之后,分别求得时间即可.
试题解析:
(1)快车速度:180×2÷(![]() )=120千米/时,
)=120千米/时,
慢车速度:120÷2=60千米/时;
(2)快车停留的时间:![]() ﹣
﹣![]() ×2=
×2=![]() (小时),
(小时),
![]() +
+![]() =2(小时),即C(2,180),
=2(小时),即C(2,180),
设CD的解析式为:y=kx+b,则
将C(2,180),D(![]() ,0)代入,得
,0)代入,得
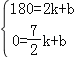 ,
,
解得![]() ,
,
∴快车返回过程中y(千米)与x(小时)的函数关系式为y=﹣120x+420(2≤x≤![]() );
);
(3)相遇之前:120x+60x+90=180,
解得x=![]() ;
;
相遇之后:120x+60x﹣90=180,
解得x=![]() ;
;
快车从甲地到乙地需要180÷120=![]() 小时,
小时,
快车返回之后:60x=90+120(x﹣![]() ﹣
﹣![]() )
)
解得x=![]()
综上所述,两车出发后经过![]() 或
或![]() 或
或![]() 小时相距90千米的路程.
小时相距90千米的路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个平面去截球,截面是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF平分∠ABE,EF=2,BF=4,求平行四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下面的解题过程的横线上填空,并在括号内注明理由
.如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.

解:∵∠A=∠F(已知)
∴AC∥DF( )
∴∠D=∠ ( )
又∵∠C=∠D(已知)
∴∠1=∠C(等量代换)
∴BD∥CE( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两商场自行定价销售某一商品.
(1)甲商场将该商品提价15%后的售价为1.15元,则该商品在甲商场的原价为 ▲ 元;
(2)乙商场将该商品提价20%后,用6元钱购买该商品的件数比没提价前少买1件,求该商品在乙商场的原价是多少?
(3)在(1)、(2)小题的条件下,甲、乙两商场把该商品均按原价进行了两次价格调整.
甲商场:第一次提价的百分率是
 ,第二次提价的百分率是
,第二次提价的百分率是 ;
;乙商场:两次提价的百分率都是
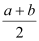 (
( .
.请问甲、乙两商场,哪个商场的提价较多?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业今年8月的产值为a万元, 9月份比8月份增加了10%,10月份比9月份增加了15%,则10月份的产值是( )
A.a(1 10%)(1 15%)万元B.(a 10%)(a 15%)万元
C.a(1 90%)(1 85%)万元D.a(1 10% 15%)万元
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数分别填入相应的大括号
﹣5,|﹣
 |,0,﹣3.14,
|,0,﹣3.14,  ,﹣12,0.1010010001…,+1.5,﹣30%,﹣(﹣6),﹣
,﹣12,0.1010010001…,+1.5,﹣30%,﹣(﹣6),﹣
正有理数集合:{________…}
非正整数集合:{________…}
负分数集合:{________…}
无理数集合:{________…}.
相关试题

