搜索
【题目】在直线AB上任取一点O，过点O作射线OC,OD，使
当
时，
的度数是（ ）
A. 
B. 
C. 或
D. 或
参考答案：
【答案】D
【解析】
分射线OC、OD在直线AB的两侧两种情况作出图形，在同一侧时，根据平角等于180°列式计算即可得解，在两侧时，先求出∠AOD，再根据邻补角的定义列式计算即可得解．
如图，
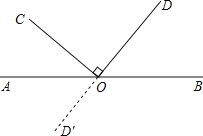
射线OC、OD在直线AB的同一侧时，
∵∠COD=90°，
∴∠BOD=180°-90°-∠AOC=180°-90°-40°=50°，
射线OC、OD在直线AB的两侧时，
∵∠COD=90°，
∴∠AOD=90°-∠AOC=90°-40°=50°，
∴∠BOD=180°-∠AOD=180°-50°=130°，
综上所述，∠BOD的度数50°或130°．
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC，AB=AC=5，BC=8，∠PDQ的顶点D在BC边上，DP交AB边于点E，DQ交AB边于点O且交CA的延长线于点F（点F与点A不重合），设∠PDQ=∠B，BD=3．
（1）求证：△BDE∽△CFD；
（2）设BE=x，OA=y，求y关于x的函数关系式，并写出定义域；
（3）当△AOF是等腰三角形时，求BE的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE，连接EB、FD，交点为G．
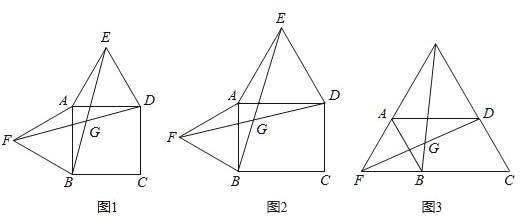
（1）当四边形ABCD为正方形时（如图1），EB和FD的数量关系是 ；
（2）当四边形ABCD为矩形时（如图2），EB和FD具有怎样的数量关系？请加以证明；
（3）四边形ABCD由正方形到矩形到一般平行四边形的变化过程中，∠EGD是否发生变化？如果改变，请说明理由；如果不变，请在图3中求出∠EGD的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“五一”小长假，小颖和小梅两家计划从“北京天安门”“三亚南山”“内蒙古大草原”三个景区中任意选择一景区游玩，小颖和小梅制作了如下三张质地大小完全相同的卡片，背面朝上洗匀后各自从中抽去一张来确定游玩景区（第一人抽完放回洗匀后另一人再抽去），则两人抽到同一景区的概率是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，一次函数
的图象与正比例函数
的图象交于点A（m，4）．（1）求m、n的值；
（2）设一次函数
的图象与x轴交于点B，求△AOB的面积；（3）直接写出使函数
的值小于函数的值的自变量x的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了倡导“节约用水，从我做起”，鼓楼区政府决定对区直属机关300户家庭的用水情况作一次调查，区政府调查小组随机抽查了其中某些家庭一年的月平均用水量（单位：吨），调查中发现，每户用水量每月均在10﹣14吨范围，并将调查结果制成了如图所示的条形统计图（不完整）和扇形统计图．
（1）请将条形统计图补充完整；
（2）这些家庭月用水量数据的平均数是 ，众数是 ，中位数是 ；
（3）根据样本数据，估计鼓楼区直属机关300户家庭中月平均用水量不超过12吨的约有多少户？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，反比例函数y=
的图象与一次函数y=kx+b的图象交于A，B两点，点A的坐标为（2，6），点B的坐标为（n，1）．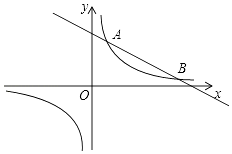 
（1）求反比例函数与一次函数的表达式；
（2）点E为y轴上一个动点，若S△AEB=5，求点E的坐标．
相关试题
