【题目】菱形ABCD中,∠ABC=60°,BD=![]() ,点E在AB上,CE=
,点E在AB上,CE=![]() ,将CE绕点C旋转60°交线段BD于F,则DF的长为 _________________.
,将CE绕点C旋转60°交线段BD于F,则DF的长为 _________________.
参考答案:
【答案】![]()
【解析】连接AC,如图所示:

∵四边形ABCD是菱形,
∴AC⊥BD,OB=OD=![]() BD=
BD=![]() ,AB=BC=CD=DA,
,AB=BC=CD=DA,
∵∠ABC=60°,
∴△ABC、△ACD是等边三角形,
∴AC=AB=CD=AD,∠ACB=∠CAD=∠ACD=60°,
∴AB= ,
,
∴CD=AB=6,
∵∠ECM=60°,
∴∠BCE=∠ACM,
在△BCE和△ACM中,
∠EBC=∠MAC=60°,BC=AC,∠BCE=∠ACM,
∴△BCE≌△ACM(ASA),
∴CE=CM=![]() ,
,
作MG⊥CD于G,设DG=x,则DM=2x,MG=![]() x,CG=6x,
x,CG=6x,
根据勾股定理得:CG2+MG2=CM2,
即(6x)2+(![]() x)2=(
x)2=(![]() )2,
)2,
解得:x=1或2,
∴2x=2或4,即DM=2或4.
∵![]()
∴![]()
∴![]()
即![]() 或
或![]()
∴![]() 或
或![]()
故答案为: ![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC是平行四边形ABCD的对角线,∠BAC=∠DAC.
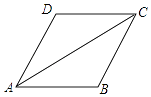
(1)求证:AB=BC;
(2)若AB=4,AC=4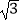 ,求平行四边形ABCD的面积.
,求平行四边形ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角三角形ABC中,AH是BC边上的高,分别以AB、AC为一边,向外作正方形ABDE和ACFG,连接CE、BG和EG,EG与HA的延长线交于点M,下列结论:①BG=CE;②BG⊥CE;③AM是△AEG的中线;④∠EAM=∠ABC,其中正确结论的个数是( ).

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形两腰上的中线相等吗?试证明你的结论
-
科目: 来源: 题型:
查看答案和解析>>【题目】商场将某种品牌的冰箱按进价提高50%作为标价,然后打出“八折酬宾,外送100元运装费”的广告,结果每台冰箱应获利300元,求每台冰箱的进价是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 通过平移或旋转得到的图形与原图形全等
B. “对顶角相等”的逆命题是真命题
C. 圆内接正六边形的边长等于半径
D. “经过有交通信号灯的路口,遇到红灯”是随机事件
-
科目: 来源: 题型:
查看答案和解析>>【题目】苏州市3月份以来,日照明显增多,日均最高气温达21℃,最低13℃,日均最高气温比最低气温高( )
A.21°CB.13°CC.8°CD.7°C
相关试题

